Ministero dell'istruzione e del merito
A002 - ESAME DI STATO CONCLUSIVO DEL SECONDO CICLO DI ISTRUZIONE
Testo valevole per tutti i seguenti indirizzi:
LI02, LI03, LI15, LI1S, LI22, LI23, LI31, LI32, LIA2, LIAO,
LIB2, LIC2, LID2, LII2, LII3, LII4, LIIS, LIS2, EA02, EA10
Disciplina: MATEMATICA
Il candidato risolva uno dei due problemi e risponda a 4 quesiti del questionario.
«La ragione non è nulla senza l'immaginazione» - Cartesio
Dati r > 0 e k < 0, si considerino la circonferenza Cr, di centro l'origine e raggio r, e la funzione fk(x) = k|x|.
a) Verificare che fk(x) è continua ma non derivabile in x = 0 qualunque sia il valore di k.
Individuare i due valori di r in corrispondenza dei quali Cr delimita con il grafico di fk, per
opportuni valori di k, un settore circolare nel semipiano y ≤ 0 di area π e contorno di
lunghezza 4 + π. Stabilito che r = 2 è il maggiore di tali valori, in uno stesso riferimento
cartesiano Oxy, tracciare la circonferenza C2> e il grafico della funzione f-1.
b) Studiare la funzione 
,
specificandone dominio, simmetrie, punti di non derivabilità, intervalli di monotonia ed insieme immagine.
Verificare che il
grafico di g coincide con la parte di C2 che si trova nel semipiano y > 0.
Spiegare perché g non è invertibile nel suo dominio ed esplicitare l'intervallo [a ; b] di ampiezza massima, con b > 0,
nel quale g ammette una funzione inversa h.
Qual è l'espressione analitica di h?
c) Sia A un punto del grafico di g, situato nel I quadrante, e siano M e R le sue proiezioni ortogonali sugli assi del riferimento. Determinare le coordinate di A in modo che il quadrilatero AMOR abbia area massima. Dopo aver verificato che tale quadrilatero è un quadrato, dimostrare che è anche quello di perimetro massimo.
d) Si consideri la funzione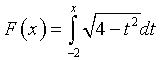 
, con x ∈ [-2; 2]. Determinare F(2)
e tracciare un grafico di F, dopo averne studiato monotonia e concavità.
Scrivere, inoltre, l'equazione della retta tangente al grafico di F nel suo punto di flesso.
« La bellezza è mescolare, in giuste proporzioni, il finito e l'infinito»- attribuita a Platone
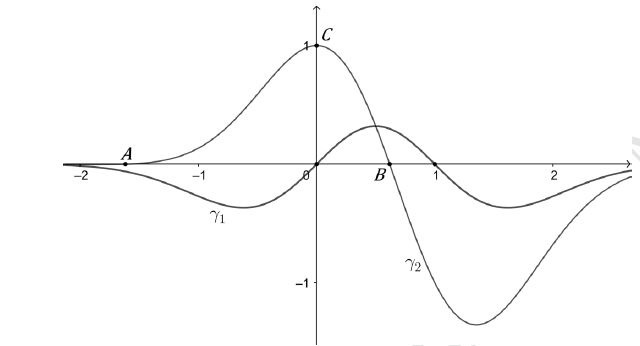
I grafici γ1 e γ2 rappresentano, rispettivamente, le funzioni f e g, definite su ℜ le cui espressioni analitiche sono
con p(x) e q(x) polinomi di secondo grado.
a) Determinare i polinomi p(x) e q(x) utilizzando le informazioni deducibili dai grafici in figura, considerando che
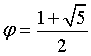è ascissa di un punto stazionario di f e che -φ,
ascissa del punto A, è uno zero di g.
b) Posto che 
, studiare la funzione f
specificando l'equazione dell'asintoto,
le ascisse dei punti stazionari e di flesso.
Verificare che la retta di equazione 
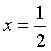è asse di simmetria
per γ1.
Determinare l'insieme immagine di f e indicare, al variare del parametro reale k, il numero di soluzioni dell'equazione
.
c) Stabilito altresì che 
,
verificare che 
è l'ulteriore zero di g
e che il triangolo ABC è rettangolo.
Dimostrare che γ1 e γ2 hanno un unico punto di intersezione, del quale si chiedono le coordinate.
Considerati su γ1 e γ2, rispettivamente, i punti P1 e P2
aventi uguale ascissa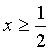 
,
calcolare la lunghezza massima che può assumere il segmento P1P2.
d) Calcolare l'area della regione limitata R compresa tra γ1, γ2 e l'asse delle ordinate.
Individuare, successivamente, il valore di 
affinché la retta x = t delimiti con i due grafici una regione R' equivalente ad R.
Dato un triangolo ABC, sia M il punto medio del lato BC e siano B' e C' due punti, rispettivamente, sul lato AB e sul lato BC,
in modo tale ch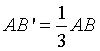e 
e
.
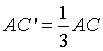Dimostrare che, se i segmenti MB' e MC' sono tra loro congruenti, allora lo sono anche i lati AB e AC.
Si considerino la superficie sferica di equazione 
e il piano π di equazione 
.
Discutere, al variare del parametro reale d, se il piano π è secante, tangente o esterno alla superficie sferica.
Determinare il valore del parametro d in modo che π divida la sfera in due parti uguali.
L'opera futurista di Boccioni "Forme uniche della continuità nello spazio" del 1913, riportata sulla moneta da 20 centesimi, descrive un uomo che avanza velocemente nello spazio.
Una parte del profilo evidenziato in figura, in un opportuno sistema di riferimento, può essere approssimato dalla funzione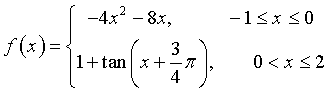 Tracciare il grafico di f, dopo averne analizzato la continuità e la derivabilità nell'intervallo [-1;2]. |
|
Assegnata una funzione g, derivabile in ℜ e tale che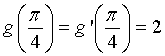 
,
determinare l'equazione della retta normale alla curva 
nel suo punto di ascissa 
.
Determinare il valore del parametro reale k in modo che le due curve 
risultino tangenti tra loro, individuando le coordinate del punto di contatto.
Scrivere una funzione polinomiale f in modo tale che la retta di equazione
sia tangente al grafico di ?? nel suo punto di ascissa 0
e si abbia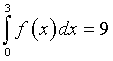 
.
Siccome mi sembrava che per puro caso alcuni fatti fossero avvenuti così com'erano stati predetti dagl'indovini,
tu hai parlato a lungo del caso, e hai detto, per esempio, che si può ottenere il "colpo di Venere" lanciando a caso quattro dadi [...].
Cicerone, De divinatione, II, 21, 48 - traduzione e cura di S. Timpanaro, Garzanti, Milano 1999.
Testo originale - Nam cum mihi quaedam casu viderentur sic evenire ut praedicta essent a divinantibus, dixisti multa de casu, ut Venerium iaci posse casu
quattuor talis iactis [...].
Cicerone, nel dialogo con il fratello Quinto, parla del colpo di Venere, che consiste nel lanciare 4 dadi a 4 facce ottenendo 4 risultati diversi. Supponendo che le facce di ciascun dado siano equiprobabili, determinare:
la probabilità di ottenere il colpo di Venere nel lancio di 4 dadi;
la probabilità di ottenere 4 numeri tutti uguali.
Quanti sono gli anagrammi, anche senza significato, della parola "STUDIARE"? In quanti di tali anagrammi si può leggere consecutivamente la parola "ARTE", come ad esempio in "SUARTEDI"? Quanti sono gli anagrammi, anche senza significato, della parola "VACANZA"?
«La matematica non conosce razze o confini geografici; per la matematica, il mondo culturale è una singola nazione» D. Hilbert
Durata massima della prova: 6 ore.
È consentito l'uso di calcolatrici scientifiche o grafiche purché non siano dotate della capacità di elaborazione simbolica algebrica e non abbiano la disponibilità
di connessione a Internet.
È consentito l'uso del dizionario bilingue (italiano-lingua del paese di provenienza) per i candidati di
madrelingua non italiana. Non è consentito lasciare l'Istituto prima che siano trascorse 3 ore dalla consegna della traccia.