si haPosto
si ha
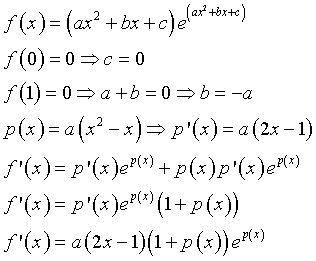
Poiché x=φ è ascissa di un punto stazionario
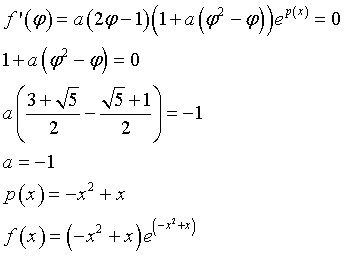
Posto 
si ha
g(0) = 1, quindi l=1, 
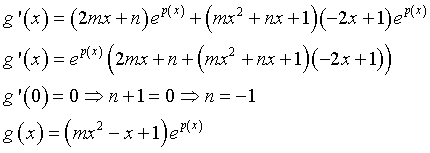
g(x) si annulla per x=-φ
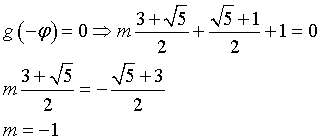
In definitiva
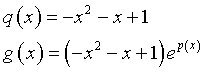
Studio della funzione 
.
f(x) è definita reale ∀x ∈ ℜ. Il fattore esponenziale è sempre > 0, quindi il segno di f
dipende solo dal segno del fattore polinomio che è positivo in ]0;1[, negativo in ]-∞ ; 0[ e in ]1; +∞[.
Il grafico interseca l'asse delle ascisse in O(0;0) e P(1;0).
Posto y=x2-x
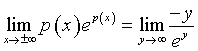
Applicando il Teorema di De l'Hôpital
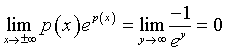
L'asse delle ascisse è un asintoto orizzontale.
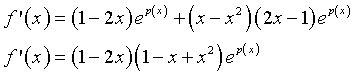
Anche in questo caso il segno della derivata dipende solo dai segni dei fattori polinomi
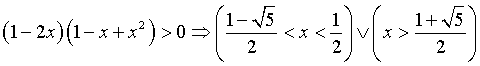
f(x) è crescente in 
,
decrescente in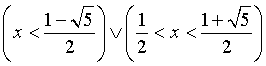 
,
ha un massimo in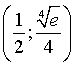 
e
minimi in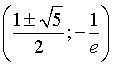 
.
Il codominio di f è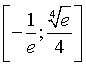 
Si ha 
, da cui
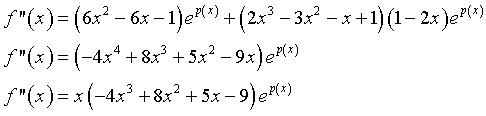
Dato che il quadrinomio si annulla per x=1
Confrontando i segni dei fattori si ottiene
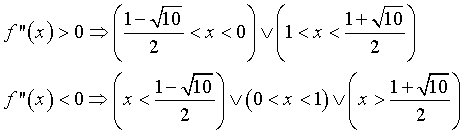
A derivata seconda positiva corrisponde concavità positiva e a derivata seconda positiva corrisponde concavità negativa. Le ascisse dei punti di flesso coincidono con estremi degli intervalli individuati.
Due punti P(x,y) e P'(x',y') sono simmetrici rispetto alla retta di equazione x=½ se hanno ordinate uguali e ascisse tali che la loro media è ½.
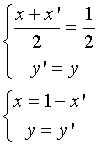
Si ottiene
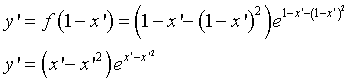
La curva trasformata coincide con la curva data confermando la simmetria.
Considerata l'equazione f(x)=k, dal grafico γ1 e indicando con C = [a;b] il codominio di f
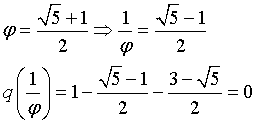
è uno zero di q.
Dati i punti A(-φ ; 0), B(;0),
C(0;1)
I coefficienti angolari sono antireciproci quindi le due rette sono perpendicolari e il triangolo ABC è rettangolo.
Le ascisse delle intersezioni tra le curve γ1 e γ2 si ottengono risolvendo l'equazione
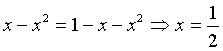
L'unica intersezione è .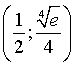
Si ha
Poiché 2x-1 ≥ 0
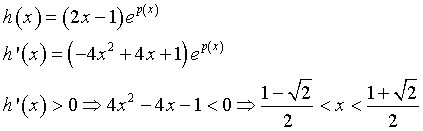
Il massimo di h(x) è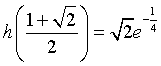 
L'area da calcolare è indicata con R e si ottiene calcolando l'integrale
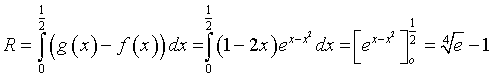
Una retta x=t (t>½) delimita con i due grafici una regione di area
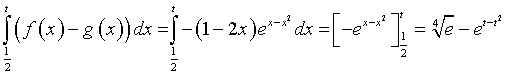
questa regione è equivalente a R se
È accettabile solo t=1.