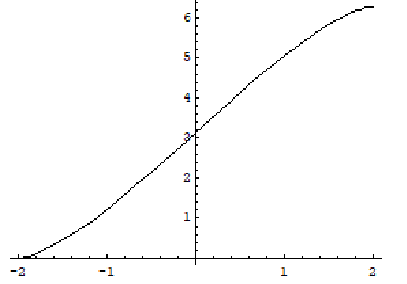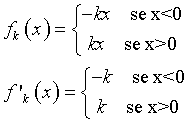
Il valore assoluto di una variabile x è definito ∀x∈ℜ, è una funzione continua uguale a 0 se il valore di x è 0, altrimenti è positivo.
Se k è negativo, la funzione fk(x) è continua e ≤0 ∀x∈ℜ.
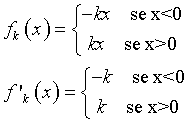
Per x = 0 la derivata sinistra di fk(x) è -k, la derivata destra è k, quindi fk(x) non è derivabile in 0 in cui presenta un punto angoloso.
fk(x) è crescente per x < 0, decrescente per x < 0 e ha massimo 0 per x = 0.
In un sistema cartesiano Oxy il grafico di fk(x) è composto da due semirette con origine in (0;0) e simmetriche rispetto all'asse delle ordinate.
Indicando con α l'angolo tra le semirette, con λ la lunghezza dell'arco da esse intercettato sulla circonferenza Cr e con σ l'area del settore circolare, si ha
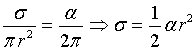
Se σ = π
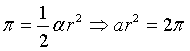
Inoltre
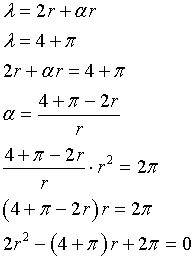
Risolvendo l'equazione di secondo grado in r si ottiene
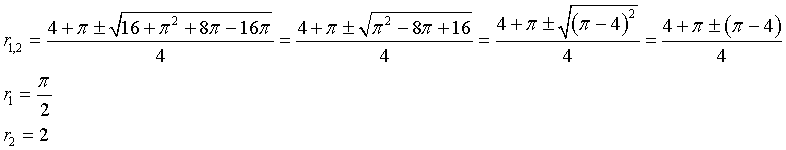
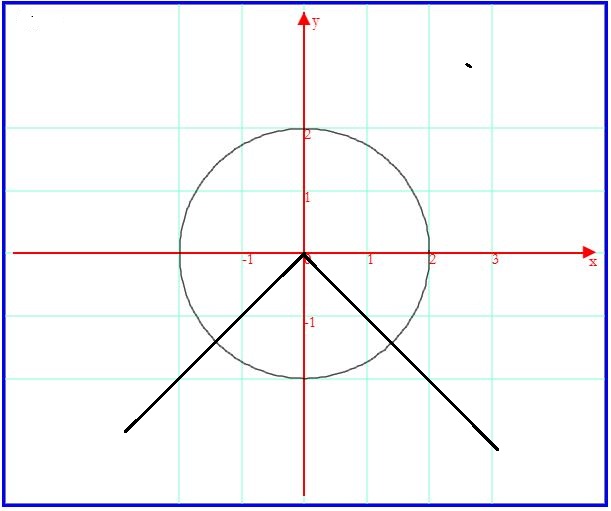
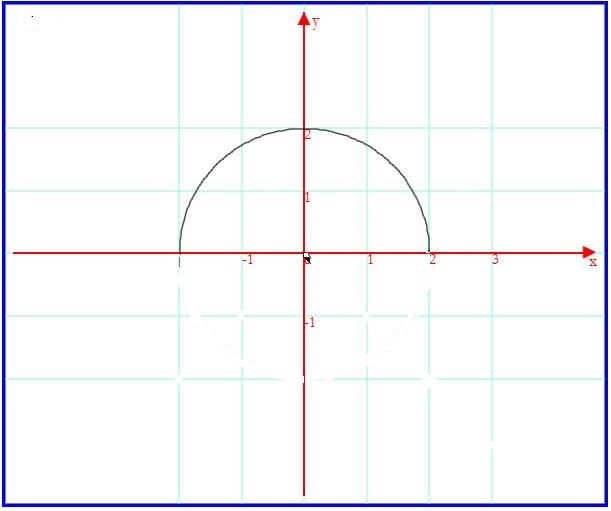
La funzione g(x) è reale per -2≤x≤ 2. In questo dominio g(x)≥0 annullandosi solo agli estremi.
Posto y = g(x), per y ≥ 0 si ha
Il grafico di g(x) coincide con la semicirconferenza costituita dall'insieme dei punti di ordinata ≥ 0 della circonferenza C2, e le proprietà analitiche di di g(x) possono essere agevolmente dedotte dal grafico osservando che essa è continua in tutto il dominio, crescente per -2<x<0, decresente 0<x<2 con un massimo in M(0;2). Le tangenti alla semicirconferenza nei suoi punti di ascisse -2 e +2 sono parallele all'asse delle ordinate, quindi g(x) non è derivabile per x = ± 2.
La funzione g(x) non è invertibile nel suo dominio in quanto non è monotòna. Per individuare un intervallo di invertibilità bisogna individuare un intervallo di monotonia, cioè un intervallo in la funzione è crescente o in cui è decrescente. Se l'estremo destro dell'intervallo deve esse positivo, l'intervallo chiesto è ]0;2[.
In questo intervallo
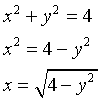
Ponendo 
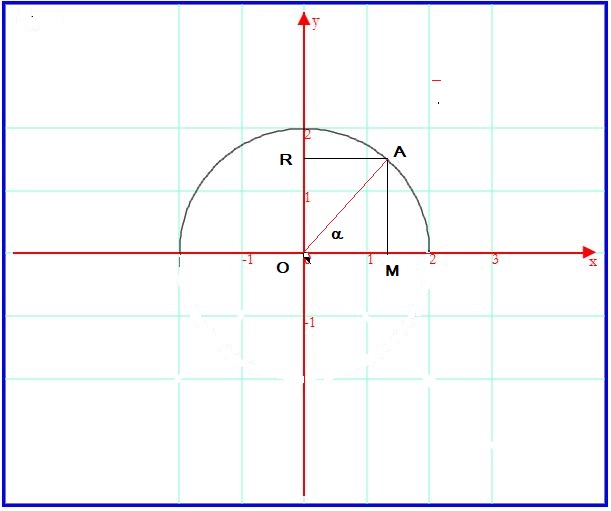
Indicando con α la misura dell'angolo AOM si ha
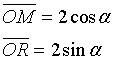
L'area del quadrilatero AMOR è
Il valore massimante si ottiene annullando la derivata prima
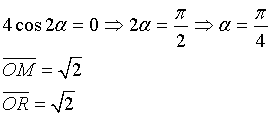
Il quadrilatero con area massima è un quadrato.
Il perimetro del quadrilatero è
Anche in questo caso il valore massimante si ottiene annullando la derivata prima
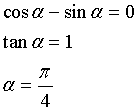
Il quadrato coincide con quello ottenuto precedentemente.
Con riferimento alla figura, indicando con P il punto di ascissa x del grafico della funzione g(x) discussa nel punto b)
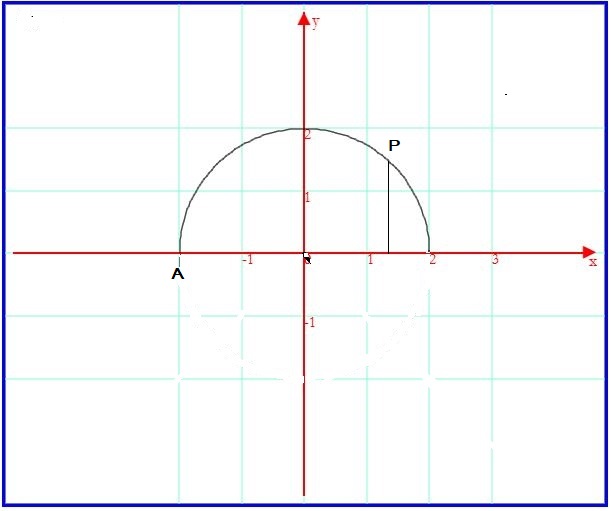
la funzion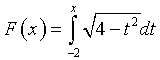e 
può essere interpretata come misura dell'area compresa
tra l'arco di semicirconferenza AP e l'asse delle ascisse e ovviamente è definita ∀ x del suo dominio e sempre crescente.
In particolare F(2) rappresenta l'area di tutto il semicerchio, quindi F(2)= 2π
Per il teorema fondamentale del calcolo integrale
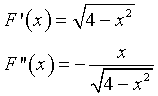
La derivata prima, positiva per tutti i valori interni del dominio, conferma che la funzione è sempre crescente.
La derivata seconda è positiva per x< 0, negativa per x> 0. La concavità è positiva nel primo semiintervallo, negativa nel secondo con un flesso obliquo nel punto F(0;π).
La tangente per F ha coefficiente angolare 2, dunque la sua equazione è
