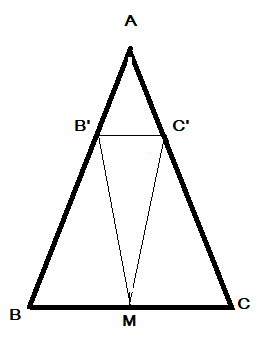
La retta del segmento B'C' che divide i lati AB e AC in parti proporzionali, per l'inverso del Teorema di Talete, è parallela alla retta del lato BC.
Per ipotesi il triangolo MB'C' è isoscele con base B'C' con angoli alla base MB'C' e MC'B' congruenti e congruenti pure con gli angoli alterni interni B'MB e C'MC.
I triangoli BMB' e CMC' sono congruenti con l'angolo di vertice B congruente con l'angolo di vertice in C quindi il triangolo ABC è isoscele.
La sfera ha centro C(1;2;0) e raggio r = 1. In generale la distanza h di un punto C da un piano di equazione ax+by+cz+d è data da
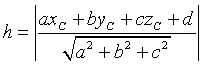
Nel nostro caso
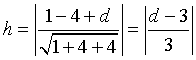
Se h = 1, il piano è tangente alla sfera
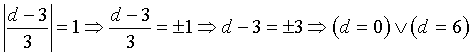
Se h < 1, il piano è secante
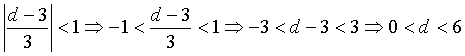
Se h > 1, il piano è esterno
Se h = 0, C appartiene al piano, cioè il piano divide la sfera in due emisferi uguali.
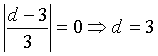
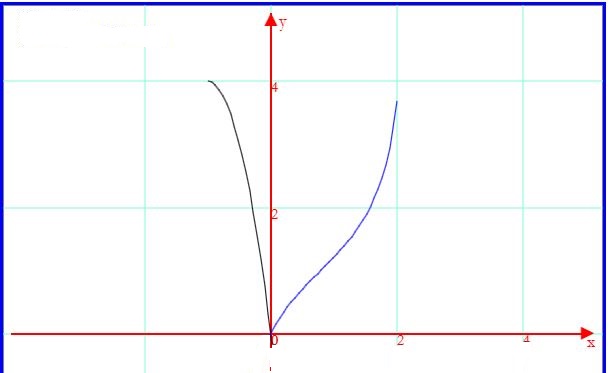
Nell'intervallo [-1,0] f(x) è rappresentata da un ramo di parabola con massimo nel vertice V(-1;4) e minimo in O(0;0).
f(x) è continua e derivabile in [-1,0[.
Nell'intervallo ]0,2] f(x) è definita per
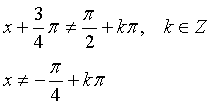
f(x) è continua e derivabile in ]0,2].
f(x) è continua per x = 0 se i limiti per x → 0 da sinistra e da destra coincidono. Poiché questi due limiti sono entrambi 0, f(x) è continua in [-1,2].
La derivata di f(x) è espressa da
f(x) è derivabile per x = 0 se i limiti per x → 0 delle derivate da sinistra e da destra coincidono ma per la derivata sinistra si ha -8 e per la derivata destra si ha 2, dunque f(x) non è derivabile per x = 0 dove il suo grafico presenta un punto angoloso.
Posto 
si ha
, quindi
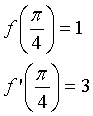
Nel punto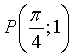 
la tangente al grafico di f(x)
ha coefficiente angolare 3 e la perpendicolare ad essa ha coefficiente angolare 1/3.
L'equazione della retta normale è quindi
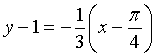
Posto
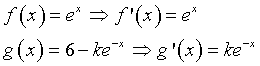
deve essere
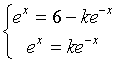
Sottraendo membro a membro
Le coordinate del punto T di tangenza sono T(0;3)
Assumendo che la funzione polinomia sia di secondo grado si pone
da cui
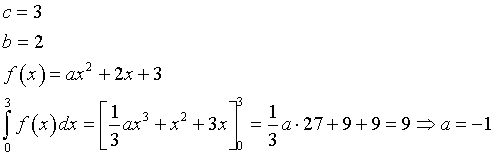
Una possibile risposta al quesito è la funzione
Gli esiti possibili del lancio di 4 dadi sono dati dal numero di disposizioni con ripetizione di 4 elementi che è dato da 44 = 256.
Il numero degli esiti con elementi tutti diversi è dato dalle permutazioni di 4 elementi, cioè 4! = 24.
La probabilità richiesta è data dal rapporto tra numero esiti favorevoli e numero di esiti possibili
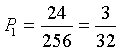
Ci sono solo 4 modi di ottenere 4 elementi coincidenti, dunque
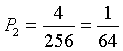
La parola STUDIARE è una sequenza di 8 elementi distinguibili. Il numero di anagrammi, cioè il il numero delle possibili permutazioni, è 8!=40320.
Il numero delle delle permutazioni contenenti la sequenza ARTE può essere calcolato considerando la sequenza ARTE come un singolo elemento da permutare con le altre quattro lettere e quindi è dato da 5! = 120.
Le permutazioni delle 7 lettere della sequenza VACANZA si ottengono dividendo le permutazioni di 7 elementi per le permutazioni delle 3 A indistinguibili e sono quindi 7!/3! = 840.