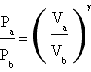
Nicolas Clément (1779-1841) and his brother in law C.B. Desormes (1777-1862), were two french entrepreneurs who started studying chemistry to improve their business. In particoular they studied gases and heat.
Their experience makes the evaluation of γ of a gas possible. γ is the ratio between the specific heat at constant pressure Cp and the specific heat at constant volume Cv of a gas, so the experience offers both a verify of the theory of perfect gases and, once accepted, a classification of every gas among those mono, di or poliatomic according to their value of γ. For example if the experience is made with the air, that is considered a diatomic gas, the theory is confirmed if the result is close to 1.4.
Cp and Cv aren't easy to measure, so the two french men thought it would have been more useful dealing with a different expression in which γ was present and in wich its value was expressed in function of quantities easier to quantify. This relation was Poisson's law for the adiabatic, P1V1 γ=P2V2γ, so they decided to divide the experiment in two following parts: in the first one they made the gas undergo an adiabatic compression wich led the gas from the initial state A to the medium state B, while in the second part they let the gas get cold (isochor cooling) till the final state C whose temperature was equal to the initial one. (the temperature in B is higher than that in A because an adiabatic compression always produces a rising in temperature. Indeed in the adiabatic ΔU=1.5RΔT=-L and being -L=PΔV always positive in case of compression also the variation of temperature must be positive that means that the final temperature must be higher than the initial one).
Poisson's law can be expressed as
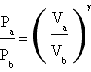
Knowing that the volume can be replaced using the equation of state for perfect gases by

the first relation results
 .
.
Completing the experience with the isochor cooling because of the law by Gay-Lussac it results
![]()
in which Tc=Ta. The ratio between Tb and Ta is in this way demonstred as equal to the ratio between Pb and Pc that let us conclude
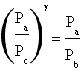 .
.
By calculating the natural logarithm of both members the equation is solved obtaining
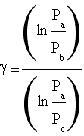 .
.
In order to make the calculation easier Pb can have the value of the atmospheric pressure while Pa and Pc can be depressions (evaluated with a liquid manometer) that can be expressed using Stevin principle as
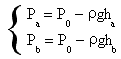
For small values of x, ln(1-x)≈-x so the numerator of the expression of γ results
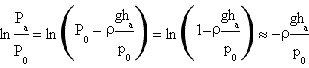
The denominator instead is
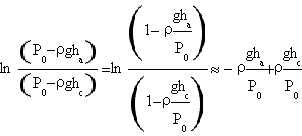 .
.
In conclusion the expression of γ is
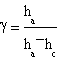
In the experiment we used a glass box closed by a gum cork through which passed two different pipes. One of them joined the box with a liquid manometer, the other with a key that made the box in contact in a first time with a Venturi's tube and in a second one with the environment.
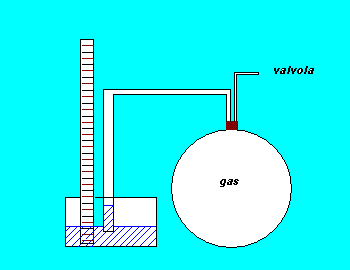
In the first step of the experience we created a
depression into the box, whose initial pressure was the
atmospheric one, using the principle of Venturi's tube.
Obtained the depression we isolated the system closing
the key and we waited until the gas lost all the heat
he had absorbed from the last process and got cool till
the ambient temperature (state A). Then we measured the
internal pressure using the manometer.
After that we started the adiabatic process that
led to the state B: we took away Venturi's tube and
opened the key letting the external air enter the box.
When the sound of the air entering the box to rise the
internal pressure till the atmospheric value stopped we
isolated once more the system (state B).
Then we just waited that the thermal balance
between the system and the environment was established
to get to the final state C. (The process BC was an
isochor cooling)
This final state was a depression (because of the law by
Gay-Lussac that adfirms the direct proportionality
between P and T in an isochor process) at the environmental
temperature. Got its pressure value with the manometer
we had all the features we needed for our
elaboration.
The process AB can be considered adiabatic because it happens so fast that it didn't let an exchange of heat between the system and the environment; the process from B to C is instead isochor because, keeping the key closed, the volume of the gas didn't change during the cooling.
Our best measures gave this features:
| ha= (33.0±0.1) cm | ha= (37.2±0.1) cm | ha= (36.9±0.1) cm |
| hc= (9.8±0.1) cm | hc= (13±0.1) cm | hc= (9.7±0.1) cm |
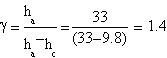 |
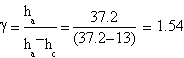 |
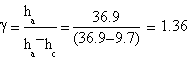 |
It is needed to use the standard deviation to associate a right error to γ value.
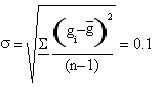
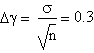
The result we got is γ=(1.4±0.3)
The result confirms our expectations because the
mean value of γ we got is the same of that
hypothesized theorically.
However the associated error is necessarily very
high.
First of all there is a strong influence on the experience of casual errors because many basical passages depends on human reflexes (such as the acts on the key especially at the end of the adiabatic process) whose precision is never reliable. In addiction the measures of the level of the liquid in the manometer could suffer from errors in their reading or could be taken before that the liquid was completely estabilished.
Moreover we must make some considerations on the fact that the air is not a perfectly diatomic gas, but just a mixture of gases among which the diatomic ones are the large majority; and on the fact that the air is a real gas and not, as contempled in the theory, a perfect gas.
A perfect gas indeed is an ideal gas formed by
punctiform molecules all with the same mass that didn't
interact the one with the others (potential energy =0)
and that have a certain speed (from which derives their
kynetic energy).
The first effort to adapt the theory of perfect
gases to the real ones was made by Van der Waals who
elaborated a variation of the equation of state for
perfect gases, but our features didn't let us expoil it
in the experience.
Van der Waals considered that each molecule had a
proper volume, that their molar density (ρ=n/V) was
important and that the molecules did interact.
His equation of state for perfect gases resulted
![]()
Where a and b are two parameters referred to the dimensions of the molecules.
The most common transformations that happen in nature are the so called irreversibile processes, that are processes that can't change the direction of their development (which is controlled by the variation of entropy ΔS) and that are so fast and chaotic that it is not possible, even knowing their initial and final state, to estabilish the values of pressure, volume and temperature for each instant of the transformation.
Hoever in particoular conditions it is possible to obtain also reversible process that are, for example, the isotherm, isobar, isochor and adiabatic transformations. The properties of these processes have been known since the XVIIIth century because they had been the objects of the studies of the founding fathers of the modern chemistry.
Boyle discovered the inverse proportionality of pressure and temperature in the isotherms
while Gay Lussac studied the isochors and the isobars and identified the direct proportionality
between pressure and temperature in the first ones, and between volume and temperature in the
second ones.
These empirical laws were later condensed in the equation of state for the perfect gases
PV=nRT
(where R is the constant of perfect gases and n the number of moles) of which they result particoular cases.
By combining the equation of state for the perfect gases with
![]()
-theorical equation obtained studying the pressure of a gas on the face of a box- it is obtained the expression of the total energy of a monoatomic gas: U=1.5 nRT.
The heat is the energy that a system exchanges with its environment in order to gain the thermical balance, that means to eliminate the difference of temperature between them.
The principle of conservation of the mechanical energy didn't talk about this form of energy so in the XVIII th century, when the first studies on thermodynamics began, it was necessary to extend it also to the thermal phenomena. The total variation of the energy of a monoatomic gas is indeed expressed by the relation
from which it is possible to deduce that a rising in temperature must correspond to a rising in the energy of the system. If the mechanical principles had been enough also in thermodynamics every rising of the temperature should have been the result of a work on the system, but it is not always true. Let's think about a pan put on the cooker. If we switch the cooker on the temperature of the pan rises, but no work has been acted on it.
In order to consider also these thermical phenomena the first principle of the thermodynamics was enounced as
where Q stands for the heat.
| ISOCORE isochor | ISOBARE isobar | ISOTERME isotherm | ADIABATICHE adiabatic |
|---|---|---|---|
 |
P1V1 = P2V2 | P1V1γ = P2V2γ | |
| L=0 quindi ΔE=Q | ΔE=Q-L | ΔT=0 quindi ΔE=0 quindi Q=L | ΔE=Q-L |
The ideas of heat and temperature are often confused in the everyday life, but in physics it is important to distinguish them. The heat is a form of energy, while the temperature is an intrinsic property of bodies and its one of their function of state (function that depends just on the state in which a body is and not on the way with which it arrived there) and can be considered as the macroscopic expression of the medium quadratic speed of its molecules.
![]()
The unit of measurement of the heat in the International System is the Joule, but also the small calorie (cal) and the large calorie (Cal) are still often used. They are defined as the amount of heat needed to rise the temperature of a g (or a Kg) of water from 14.5° C, to 15.5°C.
The absorption of heat produces in a body a variation of its temperature that is proportional to its mass; for this reason it seemed necessary to define an expression of heat that was referred to a unitary mass of each material.
This expression is the so called specific heat, that is the amount of heat needed to rise of a degree a unitary mass of a substance. If the unit considered is a mole of substance the specific heat is called molar heat.
It
is important to notice that while the specific heat changes a lot according to each element, all
the molar heat for enough high values of temperature tends to be all close to 25 j/mol, that
means that all the atoms absorb heat in the same way aside from their nature.
The more evident difference between the specific heats explains instead why, for example,
the masses of water mitigate the climate: because of their high Cs they warm up and
cool down slowlier than the other substances that form the environment around them.
The gasses are characterized from γ that is the ratio between their specific heat at constant pressure Cp and that at constant volume Cv. The value of γ was defined with the theory of perfect gasses so its practical check was a crucial experiment in order to confirm it.
Cv e Cp
In the isochor tranformations, that is in the transformations at a constant volume, of a monoatomic gas the work is null because there isn't any shifting that provokes a change in its volume. So the first principle of the thermodynamics results ΔU=Q from wich it is possible to obtain that Cv=1.5nRΔT that can be simplified in Cv=1.5R (because Cv is a molar specific heat, so n=1and ΔT=1). In the isobars transformations,that is in the transformations at a constant pressure, from the first principle of the thermodynamics it results that Q = ΔU + L, so Cp= 1.5nRΔT +L. The thermodynamic work, L, can be expressed for the isobars as
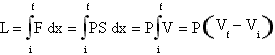 .
.
From the equation of
state of perfect gases PΔV=nRΔT, that, replaced in the last expression gives C
p=1.5R+R.
Knowing these results of Cp and Cv the value of γ for a
monoatomic gas is
![]()
On these conclusions for the monoatomic gases operated the scottish physicist James Clerck
Maxwell who formulated the principle of equipartition of the energy. This principle is based on
the rational suggestion that the poliatomic molecules can save energy also in forms different
from the translatory motion (the only one possible for monoatomic molecules that can be
considered punctiform). The diatomic molecules and the poliatomic ones should indeed save the
energy also thanks to their rotational and oscillatory motion.
In general Maxwell thought that to each degree of liberty of the speed vector of a
molecule should be associated the same constant amount of energy. This quantity
![]()
was obtained dividing into three parts (the three degrees of liberty of the translatory
speed vector) the expression of the total energy of a monoatomic gas ( U=1.5RT).
The total energy of a mole of gas resulted in general:
![]()
where f are the degrees of liberty of the speed vector.
Usually in the diatomic molecules the degrees of liberty are 5: three for the translatory
components and only two for the rotational ones (because the momentum of inertia of the rotation
on the transversal axis of the molecule is nearly null).
However, according to the quantum theory that adfirms that it is needed a minimum energy
in order to start the rotation (and, in the same way, at higher temperatures, the oscillation),
the degrees of liberty of a diatomic molecule at low temperatures are just three (those deriving
from the translation) while at a sufficient high temperature they are 6 because the oscillatory
motion starts. (If we imagine to rise the temperature even more we will arrive to the limit
passed which the oscillation is so strong that the molecule splits in independent atoms).
Nevertheless for medium temperatures and for a diatomic gas it results:
![]()
In a polyatomic gas instead the degrees of liberty are 6 because together with the three translatory components also all the three of the rotational motion are significant. For these reasons for a poliatomic gas it results:
![]()
The transformations that happen without exchanging heat with the environment are called adiabatic (from the greek a - don't diabaino - go through). For these transformations is verified Poisson's law.
P1V1γ = P2V2γ
which adfirms the inverse proportionality between P and the Vγ at which the transformation happens.
Poisson's equation is the result of the mathematical development of the equation of state of perfect gases and the first principle of the thermodynamics for the adiabatic in their differential forms.
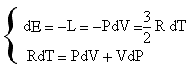
If we get from the first equation the value of dT and we replace it in the second it results:
![]()
where 5/3 is the value of γ for diatomic gases.
Dividing both members by PV it gives
![]()
wich, integrating, results
![]()
![]()
![]()
because a logarithm is constant when its argument is constant.
The scientific revolution developed a deep reflection on the method that should be peculiar to the science because the intellectuals of that time concluded that just agreeing on the process everyone could trust the results got by the others. This reflection led, for example, to the introduction of the experiment, that is a practical verify created in order to controll a theory.
Intellectuals from all over Europe took part in the debate. Among them there was Bacon, who wrote the Novum Organum in which he theorized the necessity of dividing the process into two parts, the first one, pars destruens,intent on destroying the prejudices that obscure the mind and the second one, pars construens, organized in an analytical way and in order to get the knowledge of each fenomenon with both logical and experimental processes.
Another contribute to the debate was given by Descartes who wrote the "Discussion on the method" (published in 1637 in Olland where he had moved to get the political and religious freedom that everywhere else in Europe were limited by the Counter-Reformation or the absolute monarchies) in which he not only identified the steps of the method (analysis, synthesis and revision, all based on the evidence principle) introducing the instrumental use of the doubt, but started also a research on the foundations of the method and on the possibility of extending it also to other subjects.
Also Galileo took part in the reflection because, even if he didn't deal openly with the
subject, it is possible to find notes about the method among his different works.
In the letters to Mme Cristina of Lorena, for example, he adfirmed the possibility of studying a
phenomenon starting or from sensible experiences or from necessary demonstrations. In the first
case the experiences made with the senses had to be developed into a general law from which
deduce the specifical cases to verify with an experiment; in the second instead everything
started from an hypothesys that should be demonstred.
Moreover Galileo gave a great importance to the math of which he stressed not only the
possibility of quantifying and making things measurable, as the most part of his contemporary
said, or the peculiarity of being "the language in which the Universe is written",
idea already present in Pitagora and Plato's theories, but he recognized also its creative role
noticing that it could suggest new hypothesys by developing theorically other theories.
The process that we used to find Poisson's law is a confirm of this conception of the math,
because it started from two equations and,
developing them with the only pure math, led us finding out a proportionality between the
quantities interested by an adiabatic reaction.
Under this point of view the experience of Clément Desormes is needed in order to verify
the hypothesis we reached using math as
Galileo taught us.
Moreover the experience could be considered as a crucial experiment to controll the
kinetic theory of perfect gases because it makes
possible to find the γ of a gas considered diatomic.
Knowing that the value of γ (ratio between the value of Cp and Cv)
for a diatomic gas is fixed by the theory at 1.4, if the result obtained by the experiment is
close to this value the whole theory should be confirmed.
Gas: generical name of all the substances that at ordinary values of pressure and temperature are in the aeriform state.
Looking the word gas up to the dictionary is today enough to get an orientative idea about
it, but in the past a scientific (in the modern meaning of the word) study on this subject had
been strongly delayed because of their apparent lack of weight, elusiveness and invisibility.
In the old times, in fact, their properties suggested that their nature should be divine or
similiar to the soul. Anassimene from Miles, who worked in the VIth century b.C.
identified in the air, the most common gas, the archè that his the initial element which
originated everything and gave to the animals, like a soul or a breath (pneuma), life, movement
and intelligence thanks to his own intelligence, infinity and endless movement.
In the Vth century b.C. Empedocles from Agrigentum identified in the air one of the
four roots (together with fire, water and earth) that, animated by two divine forces (filia and
meicos), were joined and separated in order to origin the life and the death of everything.
Empedocle was also the first philosopher who explained the differences between things saying
that each being was formed by the same four basical elements, but combined in different
proportions. (This is also the base for his gnoseological and nutritional theories.)
Later the theory of the four roots was taken into consideration by Aristotle (and as a
consequence accepted throughout the Middle Age in which he was considered as an auctoritas) who
quite changed it. First of all he described the differences between the roots as an effect of
the different combination of the qualities of the materia, then he divided them between active,
fire and air (whose respective qualities were hot-dry and hot-wet) and passive, water and earth
(cold-dry and cold-wet).
-The attributes that Aristotle gave to the air are more properly those of the vapor, but times
weren't ready for this distinction.-
Important observations on gas and vapor were done, in the ellenistic age, in Alessandria that became the new most important cultural center of the Mediterranean sea after the fall of the polis and the consequent decline of Athens. The city had the biggest library of the time and a museum which was used also as a school. Moreover the Maecenatism of the Ptolemei attracted there intellectuals from all over the world. Among the number of theories that were developed in Alessandria found a place both the bases of alchemy (wich was helped by the collaboration between philosophers and artisans) and scientific theories that seem to anticipate of centuries the revolution of '500/'600. Among these there were those of Erone (62/140) whose results in the studies on the compression of gases had been confirmed in the kinetic theory of gases developed in the XVIII th century. Unfortunately his studies didn't find a great success at his time because they weren't of any practical interest.
In the XIVth century, with the spreading of the plague, the conception of the air changed: the intellectuals still accepted Aristotle's vision of the air, while among the masses, that had never developed a reflection on gases, the idea that air was a way of contamination found a great fortune.
The world gas was created during the scientifical revolution by Jean Baptist van Helmont
(1577/1644) one of the first professional chemists (as he used to call himself) who, after many
studies on the combustion, created this new name from the word geist (chaos).
The concept of geist that van Helmont had in his mind was that created in the ancient
Greece (and took up again by Paracelso a few decades before) which defined the chaos as the
original element in which all the materia, that in a second step was separated in the different
beings, was initially joined. (Paracelso used this image in order to adfirm that the universe
could be studied using chemistry and not math, as the most part of the intellectuals that took
part to the scientific revolution said, and trying to pursue this aim his students created the
idea of a God, great alchemist, that, at the time of creation, separated each body from the
original chaos.)
Still during the scientific revolution the studies on pressure, made by Galileo,
Torricelli and Stevin, pointed out more accurately what a gas is.
Galileo in particular was the first who projected an experiment useful to weigh the air and to
show that the lack of weight of gases is just apparent.
In his experiment he used a precision balance on which he found the balance between a baloon
full of air and an amount of sand; then he showed that letting the gas leave the baloon the
balance was destroyed.
The following studies on gases let us know, nowadays, that the air is a mixture of gases made at the 78% of nitrogen (N2), at the 21% of oxygen (O 2) and at 1% of other gases such as the argon and the carbon dioxide. (The high predominance of diatomic gases (N2, O2) in the composition of the air makes it obey to the laws of the theories of diatomic gases.)
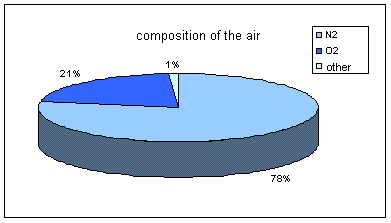
The percentages of these elements change according to the presence of different values of
water vapor, motes (mixture of dust and sand kept by the wind, pollen, mineral salts, residuals
and cinder of natural fires and vulcanic eruption) and other substances with which men pollute
the atmosphere.
The gases that men put in the air interact with its other components, change the natural
state of the echosystem and damage the life of all the beings and the human health.
In general if the polluters aren't too reactive they rise till the stratosphere where,
interacting with ozone, damage its layer; instead, if the gases tends to react
they can undergo chemical transformations and fall down on earth or can be incorporated in solid
or liquid particles and fall down later with the processes called dry-deposition and wet-
deposition (acid rain).