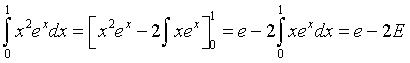
Integrando per parti si ha
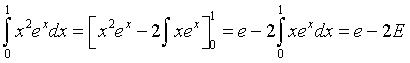
In modo analogo
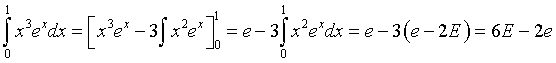
Sezione piana dei solidi su un piano passante per il raggio perpendicolare alla base della semisfera nel centro O della stessa.
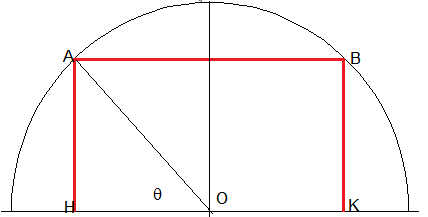
Detto r i raggio della semisfera, il suo volume misura
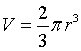
Detta θ la misura dell'angolo AOH, si ha
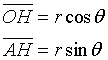
Il volume del cilindro inscritto misura
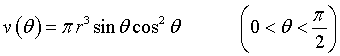
Il volume è crescente dove la sua derivata è positiva. La derivata è
![]()
Il coseno nell'intervallo studiato è costantemente positivo per cui la derivata prima è positiva per
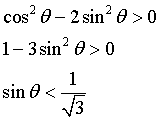
Il volume del cilindro è massimo per
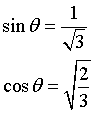
Il suo valore massimo è
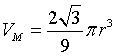
Il rapporto tra VM e quello della semisfera è
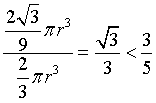
Il limite può sussistere solo se il numeratore tende a 0:
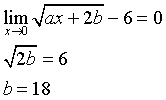
Quindi
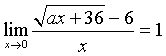
Applicando il teorema di De L'Hôpital
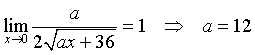
Il valor medio della distribuzione continua di probabilità è
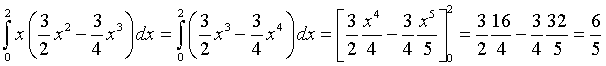
Se la densità di probabilità è continua, non ha senso chiedere la probabilità di un valore puntuale.
La probabilità della seconda estrazione non è condizionata da eventuali estrazioni precedenti, quindi la probabilità chiesta è
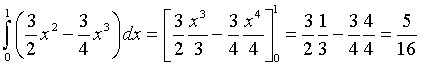
Le equazioni di una retta per due punti A e B di coordinate note sono
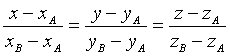
Quindi l'equazione chiesta è
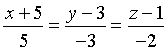
L'equazione di un piano ha forma
![]()
Il piano è perpendicolare alla retta se i suoi coefficienti a, b, c coincidono con i denominatori delle equazioni della retta, quindi
![]()
Le coordinate di C verificano l'equazione del piano, dunque
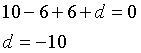
In definitiva l'equazione del piano π è
![]()
Numeratore e denominatore della frazione di cui si deve calcolare il limite sono funzioni indefinitamente derivabili entrambe convergenti a 0. Per risolvere l'indeterminazione è possibile applicare il teorema di De L'Hôpital fino a che non si trova un numeratore o un denominatore non convergente a 0.
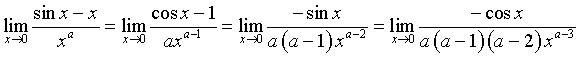
L'ultimo numeratore converge a -1. Se il denominatore diverge, la frazione converge a 0. Se il denominatore converge a 0, la frazione diverge. Perché non si verifichi nessuna di queste due ultime situazioni bisogna che l'esponente della x a denominatore sia nullo, cioè che a = 3.
Con un procedimento inverso a quello proposto nella soluzione del quesito 5, noti i coefficienti a, b, c dell'equazione del piano, si possono ricavare le equazioni di una retta perpendicolare al piano stesso.
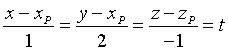
Le equazioni della stessa retta in forma parametrica sono quindi
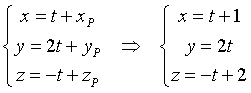
I quadrati delle distanze dei centri C delle sfere dal punto P sono uguali a 6. Dunque
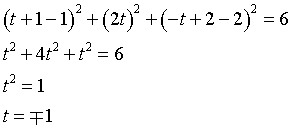
Dalle equazioni parametriche si ottengono
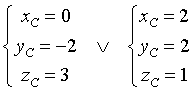
La somma delle probabilità di tutti gli eventi deve essere 1, per cui tutti i numeri diversi da 3 hanno probabilità 1/13 e il 3 ha probabilità 2/13.
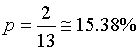
Per calcolare la probabilità che in 5 lanci il 3 esca almeno 2 volte, conviene calcolare separatamente, applicando il teorema di Bernoulli, le probabilità che il 3 non esca mai e che il 3 esca una volta, sommare queste due probabilità e poi calcolare la probabilità complementare.
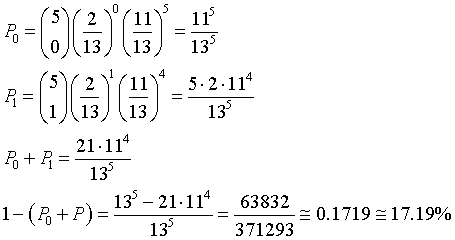
La funzione continua su tutto R f(x)
![]()
è tale che
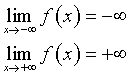
quindi, per teorema di continuità di Bolzano ha almeno uno zero. Inoltre sua derivata
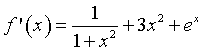
è evidentemente positiva ∀x∈R e quindi f(x) è sempre crescente e quindi può azzerarsi solo una volta.
Il grafico di f(x)
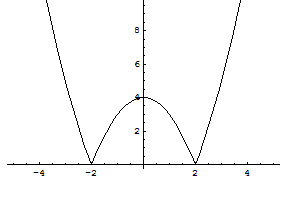
evidenzia la presenza di due punti angolosi di ascisse ±2 per i quali la funzione non è derivabile e quindi il teorema di Rolle non è applicabile.
Tuttavia il teorema di Rolle riguarda una condizione sufficiente ma non necessaria e quindi possono verificarsi situazioni, come quella proposta nella quali, anche se il teorema non è applicabile, esista un punto all'interno dell'intervallo considerato, in cui la derivata prima si annulla.