(note a cura di Roberto Bigoni)
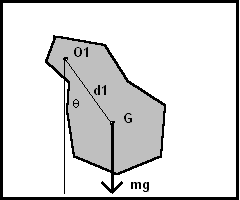
Un corpo esteso di massa m sospeso ad un punto fisso O1 nel campo di accelerazione costante terrestre g si trova in equilibrio quando il momento della forza peso P=mg applicata al baricentro G del corpo rispetto al vincolo O1 è nullo, cioè quando O1 e G sono sulla stessa verticale. L'equilibrio è stabile quando G si trova sotto O1.

Se il corpo è scostato dalla posizione di equilibrio stabile di un angolo θ l'intensità del momento della forza risulta
![]()
dove con d1 si indica la distanza tra O1 e G. Il segno negativo indica che se l'angolo θ è positivo (antiorario) il momento è negativo, cioè induce una rotazione oraria e viceversa.
Per angoli sufficientemente piccoli il seno è ben approssimato dall'angolo e si può quindi dire
![]()
Il momento della forza è la derivata del momento angolare. Indicando con I1 il momento d'inerzia del corpo rispetto all'asse di rotazione passante per O1 e perpendicolare al piano di rotazione si ha
![]()
Uguagliando i secondi membri delle (1.2) e (1.3) si ottiene
![]()
La (1.4) mostra che la derivata seconda dell'angolo rispetto al tempo è proporzionale all'opposto dell'angolo stesso. Ciò sta ad indicare che (per piccoli spostamenti iniziali) il moto del pendolo è di tipo armonico con pulsazione ω1 data da
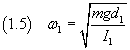
Rovesciando il corpo ed appendendolo a un punto O2 allineato con O1 e G, distante d2 da G, e lasciandolo oscillare, si ottiene una pulsazione ω2
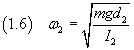
Per definizione la pulsazione ω di un moto armonico è inversamente proporzionale al periodo T
![]()
Il pendolo reversibile (di Kater: 1817) è costituito da una sbarra metallica rigida sulla quale sono incernierate due massicci dischi M1 e M2 che possono scorrere lungo la sbarra ed essere fissati in posizioni diverse in modo da mutare la posizione del baricentro del pendolo. Il pendolo è inoltre fornito di coltelli cuneiformi O1 e O2 che permettono di appoggiare il pendolo sull'apposita sede di un supporto rigido verticale e di farlo oscillare sia attorno al punto di appoggio di O1 sia attorno al punto di appoggio di O2.
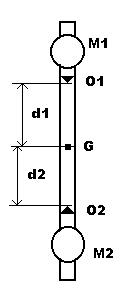
Collocando opportunamente le masse M1 e M2 è possibile fare in modo che il periodo T1 delle oscillazioni del pendolo quando è appoggiato ad O1 risulti uguale al periodo T2 delle oscillazioni che si ottengono rovesciando il pendolo e appoggiandolo ad O2.
In questo caso sono uguali anche le pulsazioni, quindi uguagliando le (1.5) e (1.6) si ha
![]()
e, semplificando,
![]()
Per il teorema degli assi paralleli (Huygens-Steiner)
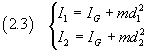
Sostituendo le (2.3) nella (2.2)
![]()
Risolvendo l'equazione (2.4) nell'incognita IG si ottiene
![]()
Sostituendo questa espressione di IG nella prima delle (2.3) si ha
![]()
e, utilizzando questa espressione di I1 nella (1.5),
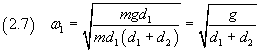
Indicando con d la distanza d1+d2 tra i due coltelli e ricordando la relazione (1.7) tra periodo e pulsazione si ottiene infine
![]()
(Nella notazione e nella semplificazione si è implicitamente assunto che la massa gravitazionale che compare nell'espressione del peso e la massa inerziale che compare nell'espressione del momento d'inerzia coincidano: la cosa meriterebbe un approfondimento...)
Questa relazione coincide con quella valida per il pendolo semplice, quando alla lunghezza l del pendolo semplice si sostituisca la distanza d tra i coltelli del pendolo di Kater e al periodo di oscillazione T del pendolo semplice si sostituisca il periodo T per il quale il pendolo di Kater è reversibile, cioè il valore del periodo comune alla oscillazioni sui due coltelli O1 e O2.
Rilevando sperimentalmente le misure di d e di T dalla (2.9) è possibile ricavare la misura di g.
Elevando al quadrato entrambi i membri si ha
![]()
e quindi
![]()
Misurando con la massima precisione possibile d e T è possibile ricavare con buona precisione il valore di g del luogo nel quale si esegue la misura.
Si ricorda che data la differenza tra raggio equatoriale e raggio polare della Terra e della forza centrifuga dovuta alla rotazione diurna la g, a livello del mare, decresce dai poli all'equatore in funzione della latitudine.
Secondo lo Handbook of the American Institute of Physics una formula empirica di g in funzione della latitudine φ è
![]()
Dalla (2.10) l'incertezza relativa sulla misura di g risulta
![]()
Per ottenere una buona misura bisogna che d e T siano abbastanza grandi e che le incertezze assolute sulle misure di d e di T siano ridotte al minimo. Per potere apprezzare la terza cifra decimale di g bisogna che l'errore relativo sia dell'ordine di 10-3.
Se d è dell'ordine del metro bisogna quindi che Δd sia dell'ordine del millimetro; se T è dell'ordine del secondo bisogna che ΔT sia dell'ordine del millesimo di secondo. Se si dispone di un cronometro manuale al centesimo di secondo si possono misurare 10 periodi e quindi dividere per 10 la misura e l'incertezza.
La misura di T è la più laboriosa per la difficoltà pratica di individuare una collocazione delle masse M1 e M2 tale per cui, capovolgendo il pendolo, il periodo rimanga invariato.
A questo scopo conviene fissare inizialmente la posizione di M1 e spostare di volta in volta la posizione di M2, cominciando dall'estremità inferiore della barra e avvicinandola gradualmente a M1, ad esempio a 10 cm alla volta. Per ogni posizione di M2 si misurano T1 e T2 compilando una tabella del seguente tipo
| M2 (cm) | T1 (sec) | T2 (sec) |
|---|---|---|
| 10 | ||
| 20 | ||
| 30 | ||
| 40 | ||
| 50 | ||
| 60 | ||
| 70 | ||
| 80 | ||
| 90 |
Si disegna poi un grafico mettendo in ascissa i valori delle posizioni di M2 e in ordinata i valori di T1 e T2 in base ai quali disegnare due curve la cui intersezione permette di valutare il valore T da usare nelle (2.10) e (3.1).
Per rendere più precisa la valutazione di T si possono infittire le misure nei dintorni del punto di intersezione, ad esempio spostando M2 di 5 cm alla volta o anche meno, e interpolare i dati con le rette dei minimi quadrati.
ultima revisione: Giugno 2020