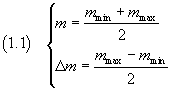
Note a cura di Roberto Bigoni
La misura esatta di una grandezza fisica è un dato teorico sperimentalmente inaccessibile e quindi sperimentalmente privo di significato.
Nella pratica sperimentale è possibile stimare direttamente solo il valore minimo e il valore massimo della misura M quindi è possibile solo affermare che M è compresa nell'intervallo [mmin,mmax].
Indicando con
le informazioni sulla misura M vengono usualmente espresse nel seguente modo
![]()
u sta per 'unità di misura' e dipende dalla unità di misura adottata per la grandezza misurata.
Il parametro Δm è detto comunemente incertezza assoluta.
Il valore di Δm definisce il numero di cifre significative con cui ha senso esprimere m, cioè l'ultima cifra significativa di M deve essere quella dello stesso ordine di grandezza di Δm.
Ad esempio non ha senso (e quindi va evitato) dire che una misura di lunghezza è
![]()
perché l'incertezza rende già poco sicura la determinazione della misura sui millimetri: le cifre relative a decimi e centesimi di millimetro sono prive di significato.
Per questo motivo è buona norma arrotondare sempre l'incertezza assoluta ad una sola cifra significativa ed esprimere come ultima cifra significativa del valor medio della misura quella su cui incide l’incertezza.
La misura esemplificata dovrà quindi essere correttamente scritta
![]()
Per stimare direttamente i valori di m e Δm usualmente si confronta M con i valori predeterminati previsti da uno strumento costituito essenzialmente da un regolo graduato (ad esempio quando si misura una lunghezza con una 'riga', con un 'metro' da falegname o con un calibro ventesimale, o quando si valuta un peso con una bilancia elettronica oppure quando si valuta una misura elettrica dalla posizione di un indice su una scala retrostante o un tempo con un cronometro).
In questo confronto ci si può trovare di fronte a due diverse evenienze:
Quando ripetendo il confronto si ottiene sempre lo stesso risultato (questo succede quando si usano strumenti poco raffinati), si assegna ad m il valore letto sullo strumento e a Δm il valore della minima suddivisione leggibile sullo strumento.
In questo caso si assume come incertezza assoluta l'incertezza strumentale.
Quando ripetendo il confronto si ottengono numerosi valori casualmente diversi (capita con strumenti molto sensibili) allora si assume come m la media della distribuzione di tali valori e a Δm il triplo della deviazione standard (σ) della distribuzione.
Nell'analisi delle distribuzioni casuali dovuta a Gauss si dimostra infatti che la probabilità che un dato sia compreso tra m-3σ e m+3σ coincide praticamente con la certezza.
Il rapporto ![]() è detto
incertezza relativa.
è detto
incertezza relativa.
L'incertezza relativa è un indice della bontà della misura.
Una piccola incertezza relativa significa una misura affidabile; una grande incertezza relativa implica una misura poco affidabile o addirittura inutilizzabile.
Dalla conoscenza del valor medio e dell'incertezza relativa è possibile dedurre l'incertezza assoluta:
![]()
Ad esempio se per una misura di lunghezza si è ottenuto per via indiretta
![]()
e su questa misura c'è un'incertezza relativa di 0.0123, si ottiene
![]()
Allora la misura deve essere scritta
![]()
Date le due grandezze omogenee A e B di misure rispettive
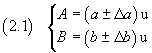
(u è l'unità di misura comune alle due grandezze che verrà in seguito sottintesa per la maggior
chiarezza del testo)
I valori minimo e massimo della loro somma S risultano
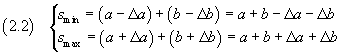
Allora il valore medio e l'incertezza assoluta di S per le (1.1) risultano
![]()
cioè
l'incertezza assoluta su una somma è data dalla somma delle incertezze assolute sugli addendi.
I valori minimo e massimo della loro differenza D risultano
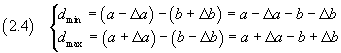
Il valore minimo di D si ottiene dal minimo di A meno il massimo di B, il valore massimo si ottiene dal massimo di A meno il minimo di B.
Allora il valore medio e l'incertezza assoluta di D per le (1.1) risultano
![]()
cioè
l'incertezza assoluta su una differenza è data dalla somma delle incertezze assolute su minuendo e sottraendo.
Date le due grandezze A e B di misure rispettive
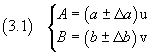
(u e v sono le unità di misura delle due grandezze, eventualmente coincidenti,
che verranno in seguito sottintese per la maggior chiarezza del testo)
i valori minimo e massimo del loro prodotto P risultano
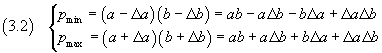
Poiché i prodotti ΔaΔb sono (per misure significative) di ordine di grandezza molto minore di quelli degli altri addendi, tali prodotti possono essere trascurati: si può quindi scrivere
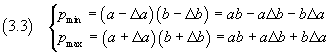
Allora il valore medio e l'incertezza assoluta di P per le (1.1) risultano
![]()
Dalla (3.4) si ottiene
![]()
cioè
l'incertezza relativa su un prodotto è data dalla somma delle incertezza relative sui fattori.
Come immediato corollario si ha che
l'incertezza relativa su una potenza è data dal prodotto dell'esponente per l'incertezza relativa sulla base.
I valori minimo e massimo del quoziente Q tra A e B risultano
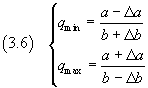
Il valore minimo si ottiene dal minimo di A diviso il massimo di B, il valore massimo si ottiene dal massimo di A diviso il minimo di B.
Il valore medio e l'incertezza assoluta di Q, per le (1.1), risultano
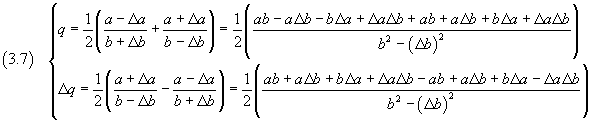
Semplificando e trascurando i prodotti e le potenze di incertezze assolute, si ottiene
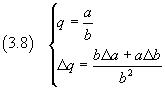
Dalla (3.8) si ottiene
![]()
cioè
l'incertezza relativa su un quoziente è data dalla somma delle incertezza relative sui suoi termini.
ultimo aggiornamento: Giugno 2020