Misura della dimensione e del peso
di una molecola di acido oleico
e stima del numero di Avogadro

(note a cura di Roberto Bigoni)

english version

1. Atomo, molecola e mole.

Già nella cultura greca classica la speculazione filosofica (Democrito, Epicuro, Lucrezio nel 'De rerum Natura'), sulla base dell'osservazione di vari fenomeni fisici (la soluzione del sale in acqua, l'evaporazione, ecc. ), aveva ipotizzato che tutti i corpi fossero composti di particelle minuscole e invisibili non ulteriormente scomponibili, denominate allora atomi ('a-tomos' = 'non tagliabile' cioè indivisibile).

La ripresa di questa ipotesi in età moderna (dal XVIII secolo) sta alla base della nascita della Chimica e della Fisica della struttura della materia.

Ma recuperando questa ipotesi gli scienziati moderni la sottrassero al campo della speculazione metafisica, nell'ambito della quale l'esistenza degli atomi fu contestata da molte scuole filosofiche rivali, tanto da essere praticamente dimenticata per quasi venti secoli, per renderla oggetto di indagine scientifica, tale cioè che le sue conseguenze fossero sperimentalmente controllabili e quantitativamente valutabili.

In particolare i chimici della seconda metà del Settecento si resero conto dei seguenti fatti.

1. Sostanze apparentemente semplici (e considerate tali per più di duemila anni, come l'acqua) potevano essere 'smontate' in costituenti ancora più semplici.

   Ad esempio l'acqua, tramite elettrolisi, può essere scomposta in idrogeno e ossigeno.

   Non è quindi legittimo parlare di un atomo di acqua. La minima particella di acqua isolabile (ma ciò vale in generale per qualunque altra sostanza) dovrà essere pensata come un aggregato particolarmente stabile di particelle più semplici al quale è stato dato il nome di molecola, mentre solo alle particelle più semplici non ulteriormente scomponibili è stato riservato il nome di atomo.

   Solo in alcuni casi abbastanza eccezionali (i gas nobili) la minima particella isolabile di una sostanza risulta non ulteriormente scomponibile in quanto formata da un singolo atomo.

   Con lo sviluppo degli studi chimici e fisici si arrivò in seguito a capire che esistono solo 92 specie di atomi stabili, mentre il numero dei vari tipi di molecole ottenibili dalle combinazioni di questi atomi è praticamente infinito.

2. Se scomponendo una sostanza si ottengono dei gas (come nel caso dell'acqua) i rapporti tra i volumi dei gas ottenuti, in uguali condizioni di temperatura e pressione, sono costanti: questa è la legge dei volumi formulata dal francese J.L. Gay-Lussac (1778-1850).

   Ad esempio, scomponendo una data quantità di acqua, il volume dell'idrogeno ottenuto risulta doppio di quello dell'ossigeno.

   Se viceversa si provoca la formazione di acqua facendo reagire due volumi di idrogeno con un volume di ossigeno, si ottengono due volumi di acqua (ovviamente ciò vale se anche l'acqua è allo stato gassoso).

3. Questo fatto ha indotto il chimico torinese A. Avogadro (1776-1856) alla formulazione dell'ipotesi che volumi uguali di gas diversi, in identiche condizioni di temperatura e di pressione, contengono lo stesso numero di molecole.

   Quest'ipotesi, in seguito a numerosi controlli, è stata assunta tra i fondamenti della scienza moderna, ed è oggi nota come principio di Avogadro.

   In base a questo principio da una data quantità di acqua è ottenibile un numero di molecole di idrogeno doppio del numero di molecole di ossigeno. Inversamente, nella formazione delle molecole di acqua, due molecole di idrogeno interagiscono con una molecola di ossigeno. Da tale reazione si ottengono due molecole di acqua.

   Studiando altre reazioni chimiche si capì che le molecole di idrogeno e di ossigeno sono, di norma, composte rispettivamente di due atomi di idrogeno e di ossigeno, risultò naturale denotare tale fenomeno nel seguente modo

   

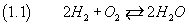
4. Se si misurano le masse dei gas contenuti nei volumi, si osserva che anche i rapporti tra le masse, in una stessa reazione, sono costanti: questa è la Legge di Proust (W. Proust, 1785-1850).

   Applicando queste leggi al caso specifico dell'acqua si conclude che la massa di una molecola di ossigeno è sedici volte quella dell'idrogeno.

5. Quindi l'atomo di ossigeno ha una massa sedici volte maggiore di quella dell'idrogeno. Studiando altri composti dell'idrogeno si giunse alla conclusione che l'atomo di idrogeno è quello che ha la massa minore.

   Venne quindi naturale assumere la massa dell'atomo dell'idrogeno come massa unitaria (u.m.a. = unità di massa atomica), in modo tale che tutte le masse degli altri atomi e delle molecole risultassero un multiplo intero di tale massa.

   La scoperta degli isotopi, cioè dell'esistenza di atomi di ugual specie chimica ma di massa diversa, portò in seguito a correggere leggermente tale impostazione, ma per gli scopi della presente trattazione e nei limiti delle approssimazioni sperimentali usate in seguito essa si può ancora assumere come sostanzialmente valida.

   Se si assume quindi come massa unitaria quella di un atomo di idrogeno, la molecola biatomica dell'idrogeno ha massa 2 u.m.a.

6. Se si considerano 2 g di idrogeno alla temperatura di 0°C e alla pressione di 1 Atmosfera (condizioni normali), si constata che questa quantità di gas occupa un preciso volume (circa 22,4 litri) e, per il principio di Avogadro, sarà formata da un ben preciso numero di molecole.

   Tale numero di molecole è detto numero di Avogadro.

   Anche se si prendono 32 grammi di ossigeno, ad uguale pressione e temperatura, si osserva che questa quantità di gas occupa lo stesso volume e deve essere formata da un ugual numero di molecole.

   In generale una quantità di una sostanza formata da tante molecole quante ce ne sono in 2 g. di idrogeno è detta mole.

   Tutte le sostanze allo stato gassoso, in condizioni normali, occupano lo stesso volume di circa 22.4 litri, detto volume molare.

   In conclusione, per capire quanti grammi di sostanza sono necessari per averne una mole, se la sostanza è gassosa, si misura il peso di un volume molare;
   altrimenti è necessario sapere di quali e quanti atomi è composta la sua molecola, calcolare a quante u.m.a. corrisponde la somma delle masse degli atomi (peso molecolare) e considerare un numero di grammi uguale a tale somma.

Ad esempio, la molecola di acido oleico (sostanza liquida a temperatura ambiente, molto usata nella cosmetica per saponi e creme) è un aggregato di 18 atomi di Carbonio, 34 atomi di Idrogeno e due atomi di Ossigeno e viene quindi denotata con C₁₈H₃₄O₂.

Se la massa dell'atomo di Carbonio fosse 12 u.m.a., quella dell'atomo di Idrogeno 1 u.m.a. e quella dell'atomo di Ossigeno 16 u.m.a. , per avere una mole di acido oleico bisognerebbe prendere 282 g di acido oleico. In effetti, data l'esistenza di isotopi, la u.m.a. non coincide esattamente con la massa dell'atomo di Idrogeno e, ad esempio, la massa dell'atomo di Carbonio non è esattamente 12 u.m.a. (è molto noto, ad esempio, il Carbonio 14) e quindi una mole di acido oleico risulta più esattamente 282,5 g.

2. Stima delle dimensioni e della massa delle molecole di un liquido e del numero di Avogadro.

È praticamente impossibile con mezzi ordinari isolare una singola molecola per renderla oggetto di uno studio quantitativo delle sue proprietà.

Per alcune sostanze è tuttavia possibile con diverse metodologie ottenere strati talmente sottili da rendere plausibile l'ipotesi che lo strato sia quasi o certamente unimolecolare.

Ad esempio Rutherford progettò la sua celebre esperienza, che portò alla comprensione della struttura interna dell'atomo, sparando particelle α contro un sottilissimo strato di oro.
Ma la possibilità di laminare oro in strati così sottili richiede strumentazione non usualmente disponibile.

Con i liquidi la cosa è più semplice.
Se due liquidi hanno diversa densità (massa specifica) e non si mescolano, posti nello stesso recipiente, nello stato di equilibrio, si dispongono in strati separati, con il liquido meno denso sovrastante quello più denso.
Il liquido poco denso e non mescolabile con l'acqua che verrà usato nella misura successivamente descritta è l'acido oleico, quindi da ora in poi, per dare maggiore concretezza alla trattazione, si fa riferimento a tale sostanza.

Lo spessore di ogni strato dipende dalla quantità di liquido usata.

Se si usa una quantità di acido oleico così piccola da non permettere la formazione di uno strato che copra totalmente la superficie del liquido sottostante, ma solo di una 'macchia' che lo copra parzialmente, appare ragionevole l'ipotesi che la 'macchia' sia formata da uno strato unimolecolare.

Se si conosce il volume V di acido oleico usato e si riesce a stimare l'area S della superficie della macchia, è possibile ottenere lo spessore d della macchia stessa che dovrebbe ragionevolmente coincidere con lo spessore di una molecola

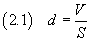
Se ora si suppone che la molecola abbia forma di cubo, si può stimare il volume v della molecola

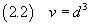
e, se si conosce la densità ρ dell'acido oleico, se ne può stimare la massa m

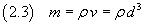
Se poi si conosce la massa M di una mole di tale sostanza è possibile stimare il numero di Avogadro N

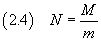
3. Incertezze sulle misure fisiche.

La relazione (2.1) è puramente concettuale, ricavata dalla geometria euclidea. Teoricamente la misura di una grandezza geometrica è data da un numero reale, razionale o irrazionale a seconda che essa sia commensurabile o meno con l'unità di misura.

Nella pratica sperimentale il valore teorico di una misura non è mai accessibile.
L'unica cosa che si può fare è stabilire un estremo superiore e un estremo inferiore al valore di tale misura, cioè stabilire un intervallo al cui interno cade con ragionevole sicurezza il valore della misura.

Nel caso qui esaminato, cioè la misura della superficie coperta da 'una macchia' di acido oleico, il problema si pone in modo evidente.

Tale superficie ha di solito una forma molto irregolare, non riconducibile alla figure teoriche studiate dalla geometria piana e quindi non ottenibile tramite le misure di segmenti.

Per stimare l'area di tale superficie si può ricorrere al seguente metodo: si pone sotto al recipiente contenente i liquidi un foglio di carta millimetrata.
Se i liquidi sono trasparenti è possibile vedere il foglio.
Si conta il numero di quadretti di un cm di lato completamente contenuti nel perimetro della macchia (q) e poi il numero di quelli interni o attraversati dal perimetro della macchia (Q).

Dopo questo conteggio si può dire che l'area S è compresa nell'intervallo [q;Q] cm².

Se si indica con s la semisomma tra q e Q e con Δs la semidifferenza tra Q e q, si può equivalentemente dire che l'area è compresa nell'intervallo [ s-Δs ; s+Δs ] cm².
Lo stesso concetto può essere più brevemente espresso dicendo che

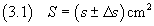
La (3.1) è il modo usuale di esprimere le misure fisiche.

Nella (3.1) s è il valor medio della misura, Δs è l'incertezza assoluta.

La misura di S è tanto più precisa quanto più è piccolo il rapporto

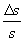
Tale rapporto è detto incertezza relativa.
Se si volesse, con lo stesso metodo indicato, ottenere una misura più precisa, si potrebbero contare, invece dei quadretti di 1 cm² individuati dal contorno della 'macchia', i quadretti di 1 mm².
L'operazione risulterebbe un po' più laboriosa, ma porterebbe ad una incertezza relativa molto minore, cioè ad una misura molto più precisa.

4. Valutazione statistica dell'incertezza.

Un metodo molto più significativo e produttivo (ma più laborioso) per stimare l'area S è quello statistico.

Ripetendo più volte la deposizione di volumi uguali di acido sulla superficie dell'acqua, si otterranno macchie di area S diversa.
La grandezza S si comporta come una variabile casuale. L'analisi teorica del comportamento delle variabili casuali condotta dal matematico K.F. Gauss (1777-1855) porta alla conclusione che la miglior stima della misura è fornita dal valor medio della distribuzione dei valori ottenuti e che l'incertezza assoluta è stimabile pari al triplo della deviazione standard della distribuzione.

(Per ottenere velocemente valor medio e deviazione standard sono utili le funzioni statistiche di un foglio elettronico).

5. Misure di volume.

Anche la misura del volume della 'macchia' richiede particolari accorgimenti.

Innanzitutto questo volume deve essere molto piccolo, altrimenti la macchia si allargherebbe a tutta la superficie disponibile, facendo cadere l'ipotesi dello strato unimolecolare.

Per ottenere un volume sufficientemente piccolo di acido oleico, invece di estrarre direttamente una quantità di acido dal recipiente che lo contiene, si diluisce tale acido in un liquido molto volatile (ad esempio il pentano), tale che, una volta depositata una quantità di soluzione sull'acqua, il solvente evapori velocemente e rimanga sull'acqua solo l'acido oleico. Per diminuire maggiormente il volume di acido si può ricorrere a diluizioni successive.

Concretamente, si prepara prima una soluzione di 1 ml di acido oleico in 99 ml di pentano: in tale soluzione c'è quindi lo 1% di acido oleico.
Poi si prende 1 ml di tale soluzione e la si diluisce in 99 ml di pentano. In questa seconda soluzione solo una parte su 10000 è di acido oleico.
Se si prelevano 0,2 ml di questa seconda soluzione per formare la macchia, il volume di acido oleico usato è un decimillesimo di 0,2 ml.

1 ml equivale ad 1 cm³, quindi il volume di acido oleico usato risulta 2.10^-5 cm³.

Ma anche su questa misura c'è un'incertezza assoluta.
Se, ad esempio, per estrarre tale quantità di soluzione si usa una pipetta graduata in decimi di ml e si traguarda la superficie della soluzione su una tacca della pipetta, una fonte di incertezza sulla misura è dovuta al menisco che la superficie della soluzione forma nella pipetta. Supponendo che l'incertezza assoluta sia almeno di un decimo di ml, il volume di acido oleico deve essere stimato in

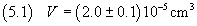
6. Propagazione delle incertezze.

Se, ad esempio, con il volume (5.1) di acido si ottiene una macchia di superficie

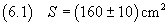
è possibile stimare la misura dello spessore in

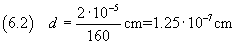
Ma, ovviamente, da dati incerti non si può ottenere una misura certa.

L'incertezza su tale misura può essere ottenuta applicando le regole sulla propagazione delle incertezze: in particolare l'incertezza relativa su un quoziente è data dalla somma delle incertezze relative sui termini.

Quindi

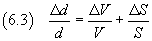
Nel caso proposto

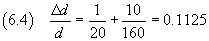
L'incertezza assoluta è quindi 0.1125·1.25 10^-7 cm, cioè circa 0.14·10^-7 cm.
L'ordine di grandezza dell'incertezza assoluta è un decimo di quello della misura: hanno senso solo le cifre di ordine di grandezza maggiore o uguale a questo. Quindi si arrotondano le misure a tale ordine di grandezza.

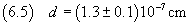
Nell'ipotesi che la molecola di acido oleico sia cubica, si può calcolare il suo volume usando la (2.2).

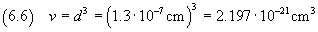
L'incertezza relativa sul volume risulta tripla dell'incertezza relativa sullo spigolo, cioè 0.3375.

Allora l'incertezza assoluta risulta 0.74·10^-21 cm³ e quindi la misura del volume è espressa da

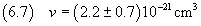
La densità dell'acido oleico è

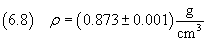
e quindi dalla (2.3) si ricava la massa della molecola

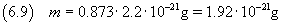
L'incertezza relativa su un prodotto, come per il quoziente, è data dalla somma delle incertezze relative sui fattori. In questo caso coincide praticamente con l'incertezza relativa sul volume (0.3375) e quindi

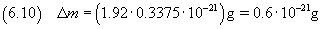
In definitiva

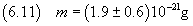
A questo punto si può stimare il numero di Avogadro dividendo la massa di una mole per la massa di una molecola, secondo la (2.4)

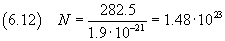
L'incertezza relativa è sempre circa 0.3375, quindi l'incertezza assoluta è circa 0.6·10²³

In definitiva si ottiene

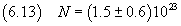
Questo valore coincide con quello ottenuto con misure più raffinate (circa 6·10²³) per quanto riguarda l'ordine di grandezza, ma è decisamente insoddisfacente per quanto riguarda la mantissa.

Molto probabilmente la discrepanza è dovuta al fatto che si è arbitrariamente ipotizzato che la forma della molecola fosse cubica.

Ipotizzando che altre figure geometriche solide approssimino meglio la forma della molecola si possono ottenere valutazioni migliori.

Ad esempio, se si suppone che la forma della molecola assomigli ad un ottaedro costituito da due piramidi simmetriche a basi quadrate coincidenti di lato d e alte entrambe d/2 il volume e massa risultano un terzo di quelli del cubo e quindi la valutazione del numero di Avogadro e della sua incertezza risultano triple rispetto a quelle stimate nella (6.13). Si ottiene cioè

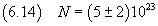
I lavori degli studenti

• primo
• secondo
• terzo

ultimo aggiornamento: Giugno 2020