A pendulum is a body which moves with harmonic motion, that is with a motion repeted at regoular intervals. This motion is generated by the action of an elastic force which, obeying Hooke's law F=-kx, is always proportionated to the opposite of the displacement from the position of equilibrium of the body.

Galileo, interested in a mathematical approach to the study on motions, was among the firsts who studied and realised pendulums. It seems that the interest in this tool was born after the observation of the oscillation of a lamp hung from the ceiling of the cathedral of Pisa. Deeper studies let him identify the relations between the period, the mass and the length of a pendulum and find out its isochronism (that is the indipendence of the period from the amplitude of the oscillation). This proprety, however, was limited in the following decades by Huygens who demonstred that a pendulum is perfectly isochronous just for small oscillations. For small oscillations the period results:
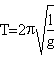
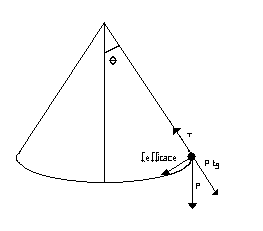
In order to demonstrate this equality we could imagine to study an ideal pendulum composed of a inextensible and massless thread and a punctiform, but dotated of mass, body hung by it and free to oscillate around its bond.
If we immagine to displace the pendulum from his position of equilibrium, where the weight of m is perfectly balanced by the tension of the thread, the same weight will be resolved into its radial and tangential components.The first one will be still balanced by the tension , but the second will be completly unopposed and will become the effective force which act on the pendulum.
The modulus of this force is F=mgsinθ, where θ is the angle of oscillation. As long as the amplitude of the oscillation is small, (θ->0) as that we consider, θ tends to be equal to sinθ so the modulus of the force can be expressed by F=mgθ.
θ is also the central angle of a semicircular sector whose value can be represented by the relation:
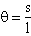
(where s is the arch described by the mass during its displacement, and l the length of the thread). Than the modulus of the effective force acting on the pendulum is
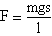
whose direction is opposite to the way of displacement. This expression of the effective force describes it as an elastic force proportioned to the opposite of the displacement accordong to the constant
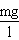 .
.
Equalizing Hooke's law to the second principle of the dynamics the modulus of the acceleration results
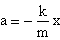 .
.
In the harmonic motions a=ω2x so it is possible to conclude that
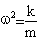
K in this case can be replaced by
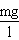
in order to say that ω 2 of a pendulum is g/l. The initial equation
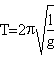
results demonstred by rimembering the relation between ω and the period (ω=2π/T).
This equation make it possible to find out the experimental value of g, however the ideal pendulum cannot be used to pursue this aim because its faithful realization is impossible.
The studies on pendulums were carried on in the following decades by Christian Huygens Dutch astronomer and scientst. He managed to complete Galileo's project about the reallization of a clock based on pendulums. In order to do that he used and applied also Galileo's studies on the cycloid.
He understood that the circular pendulum was isochronous just as long as the amplitude of the oscillations was small, whyle the construction of the gears for clocks needed the use of a pendulum isochronous for any oscillation. To create it he applied two cycloidal guides in the point of suspension so that the curve originated was a cycloid too.
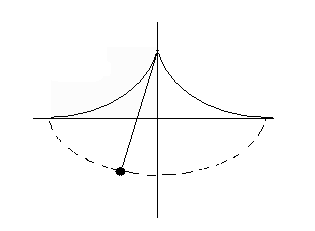
With this devices he was the first who built a truly isochronous pendulum which gave benefits not only to the clockmaking but also, for example, to the navigation because it made possible the knowledge of the spacial coordinates of a body and verified the variation of the acceleration of gravity according to the latitude.
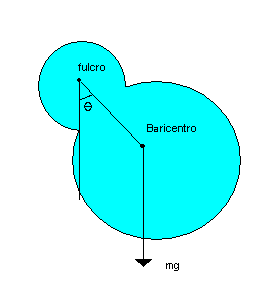
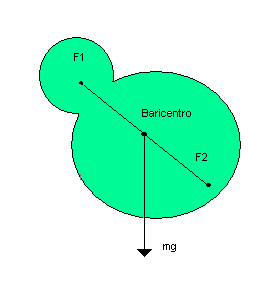
The real pendulum is an extended body free to oscillate around a fixed point. The steady equilibrium of this body is got when its barycentre is lined up with its bond.
On the body acts the weight force, which can be considered applied to the barycentre of the body, that coincide with its centre of mass if it is not so large to be thought as affected by different local values of g.
A θ displacement of the pendulum from its position of equilibrium makes the torque of this force Τ=-dmgsinθ where d is the distance between the bond and the barycentre and the minus, according to Hooke's law, imply that if &thet; is positive, that is the result of an anticlockwise rotation, the origined rotation will be clockwise and vice versa.
As already said sinθ and θ tend to cioncide as long as θ->0, so Τ=-dmgθ.
The angoular moment is at the same time the integral of the torque and the derivative of the moment of inertia calculated fror the axe passing its bond
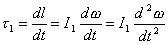
so equalizing these expressions it results
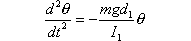
This differential equation shows that the motion of the pendulum considered is a harmonic motion in which
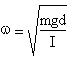
The theory of the moments of inertia (I) was introducted by Huygens in his book “Horologium oscillatorium”,dedicatyed to Luis XIV, and was deepened with Steiner's contribution in the formulation of the theorem of parallel axes which affirm that:
The moment of inertia of a body which rotates on any axe is equal to the sum of the moment of inertia calculated for the parallel axe passing its centre of mass and the product between the total mass of the body and the square of the distance between its c.o.m and the point passed by the first axe.
These studies were necessary for Kater (English geodesist lived between 1777 and 1835) to use advantageously the relation
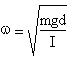 .
.
Finding out I is quite difficult so he created a new model of pendulum that let him equalize I with an expression of quantifiable data. This pendulum is known as reversible.
The reversible pendulum is a massive staff provided with cuneiform knives which can become alternatively the point of oscillation of the pendulum. On the staff there are two masses one fixed and the other free to run between the knives so that the position of the barycentre of the body is affected by the place they are.
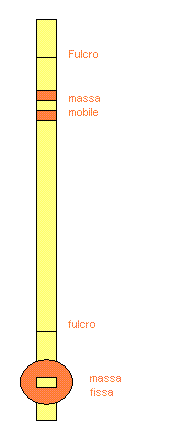
Kater demonstred that finding the position of the free mass wich make equal the period of oscillation of the pendulum on both bonds it is possible to replace I with a quantifiable expression. In fact once obtained the condition of equality between the periods it is possible to deduce also the equality of the pulsatances ω:
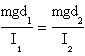
where d1 and d2 are the distances between the barycentre and the bonds(O1 and O2). Simplifying it results I1d2=I2d1. For the theorem of Huygens-Steiner

which, replaced to the last equation, gives
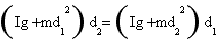
If this expression is solved using Ig as unknown it is Ig=m1d2. The theorem of parallel axes then can be expressed with
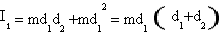 .
.
The demonstrationof this equality let Kater replace I with a easly measurable value:
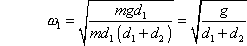
d1+d2 can also be replaced by d, distance between the wedges, because this is perfectly equal to the sum of the distances beween each wedge and the barycentre because they lined up with each other and, at same time, with it.
Got the pulsatance and remembered its relation with the period
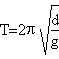
it is possible to find the local value of g measuring the period of oscillation of a pendulum.