The hyperbolic sine is an always increasing function, therefore it is bijective and invertible over all ℜ. If we denote by arcsinh its inverse function, we can write
![]()
From the second one of the (3.9), remembering that ey>0, we have
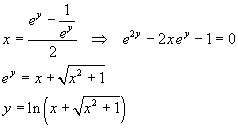
and finally
![]()
The hyperbolic cosine isn't monotonic, so it isn't invertible over all ℜ; to make it invertible we must restrict its range to non negative arguments. Only in this case we can have its inverse function, denoted by arccosh.
![]()
From the first one of the (3.9), excluding the negative y,
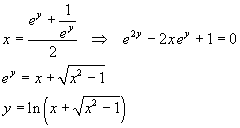
and finally
![]()
The hyperbolic tangent is an always increasing function, therefore it is bijective and invertible over all ℜ. If we denote by arctanh its inverse function, we can write
![]()
From the third one of the (3.9), remembering that e2y>0, we have
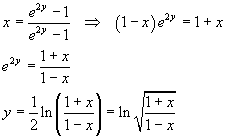
![]()