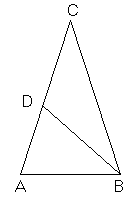
All the isosceles triangles in which the angles at the base are the double of the angle at the vertex can be called golden triangles of the first type.
The sum of the inner angles of a triangle is π, therefore the angle at the vertex has measure π/5 (36°) and the angles at the base have measure 2π/5 (72°).
The reason of the attribute 'golden' resides in the fact that in such triangles the base is the golden part of the side.
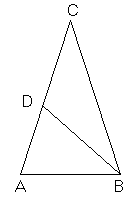
Tracing the bisector from the vertex B which intersects the opposite side in D, the triangles ABC and ABD turn out similar. We can therefore write the proportion
![]()
Triangles ABD and BDC turn out both isosceles: in particular the segments AB, BD, DC turn out to be congruent. We have therefore AD = AC-AB. Then the base AB is equivalent to the golden part of side AC.
The triangles similar to triangle BCD, i.e. the isosceles triangles in which the angle at the vertex is the triple of the angles at the base, are called golden triangles of the second type. In these isosceles triangles the side is the golden part of the base.
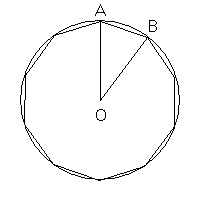
An immediate consequence of this property of the golden triangles of the first type is that the side of the regular decagon inscribed in a circumference is the golden part of the radius.
A regular decagon can be divided in ten golden triangles having the bases on the sides and the centers in common. The equal sides of the triangles coincide with radii of the circumscribed circumference.
The measure of the side of the decagon turns out to be
![]()
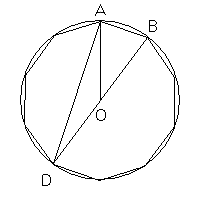
Extending the radius BO until the diametrically opposite point D and tracing the segment DA we get the rectangle triangle BAD the hypotenuse of which is the diameter BD and in which the acute angle in D has the measure π/10 (18°); the value of the sine of π/10 (18°) can therefore be deduced
![]()
From the sine we can immediately deduce the cosine.
![]()
The measure of the segment AD turns out to be
![]()
Indicating with C the middle point of the minor of the arcs AD, the triangle ACD turns out to be a golden triangle of the second type. The segments AC and CD are sides of the inscribed regular pentagon. The segment AD is one of the diagonals of such pentagon. Therefore the side of the regular pentagon inscribed in a circumference is the golden part of its diagonal.
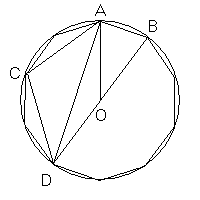
The measure of the side of the pentagon turns out to be
![]()
If we draw the diagonals of a regular pentagon we obtain the stellar pentagon, which was the symbol of the Pythagoras school and to which was attributed exoteric meaning in hermetic, kabbalistic and masonic tradition.
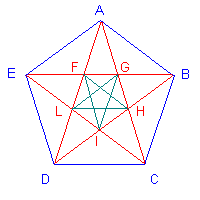
In this figure the segment AE is the golden section of the segment AD, the segment AF is the golden section of the segment AE, the segment FG is the golden section of the segment AF. If one draws the diagonals of the pentagon FGHIL and, after, the diagonals of the new pentagon made by them an so on, the sequence can continue infinitely.