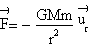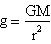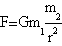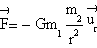Acceleration of gravity
g: acceleration of gravity
By acceleration of gravity is meant that acceleration which affects the bodies speed during the free fall (due to their weight).
The direction of g is the straight line (the motion of fall of bodies can be considered as a particoular case of the rectilinear uniformely accelerated motion) that join the body to the center of Earth which is also the point the way of the g vector is directed to. Near the surface of the Earth the modulus of the acceleration of gravity is (9.80665±0.00001)m/s2.
This value has been worked out by the analysisof the world gravimetrical net, traced thanks to the cohoperation between international bodies in the survey of the local acceleration of gravity all over the world. (Italy has played an important role in this surveys because the first evaluation of g in the antartic area was made in the italian base of Terranova's Bay.)
g is not constant everywhere because it depends on many factors which change according to the area so it is impossible to give an absolute value of it.g depends, for example, on:
- the fact that the density of Earth is not homogeneous because of its internal structure and of the presence beneth the surface of deposits which affect the value of g.
- The Earth spins around its rotation axis, which join the Poles and is inclined compared to the ecliptic plane, so every body on its surface issubjected not only to the acceleration of gravity but also to the centripetal acceleration due to this rotation.
- The Earth is not a perfect sphere because it is squashed at the Poles and there are relieves and depressions on its surface.
The law of universal gravitation by Newton
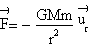
where M is the mass of the Earth, m the mass of a body on its surface and r the distance between the body and the center of the Earth) can be equalled to the weight force applied to the same body placed on the surface (it is possible to do that because both the forces exspress the attraction that the Earth practices on the body) in order to obtain that
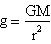
g can't be constant because r2 changes according to the latitude and altitude of a place. (Last exspression has been simplified dividing both members over m, operation that became possible only after Eövos' exsperiments whichproved that gravitational and inertial mass can be considered equal.
In his description of the natural motions Aristotle said that they were just of two types: cyrcular, the one of planets,perfect and ethereal, and vertical, the one of physical bodies which, according to their weight, fell down or took off.
Moreover the weight of each body, in Aristotle's opinion, affected not only the direction of the fall, but also its speed and the heavier they were, the faster they fell.

This theory had a great fortune until the 17th century when it was confuted by Galileo.
Indeed he affirmed that if we imagine three blocks (made out of the same material, and equal in form and dimensions) free to fall down in the vacuum there are no reasons to believe they will fall at different speeds.
Then he observed that if bodies with different velocities are joined together the slower retards the other, but if are joined bodies with the same velocity the system obtained doesn't neither speed up nor slow down. This condition let him conclude that if we imagine to tie two of the three previous mentioned blocks, and to let this system fall together with the rimaining block in frictionless condition (whose effect wuoldn't have been the same on the block and on the system) we should expect to see them falling at the same speed.
By this demostration he confuted not only Aristotle's theories, but also those positions that affirmed the existence of an acceleration dependent on the weight of a body.
Then he is said to let fall from the tower of Pisa (city in which he was born on the 15th of february 1564) blocks made out of different materials, but with the same form and dimensions so that the air friction affected their fall in the same way, and he noticed that it was impossible to distinguish defferent variation of speed during their fall so he understood that acceleration which he had already set free from the weight of a body was indipendent also from its composition and its form.
He came to the conclusion that all the bodies which are falling near the surface of the Earth are affected by the same acceleration.
So it was Galileo the first who knew and demonstred the existence of g and its local canstance (it's indipendent from all the intrisic characteristics of a body so it acts on everything in the same way) but he couldn't manage to discover its variation due to latitude and altitude.
- Even if Galileo had lived ages before the complex internal structure af the atom was discovered, his experiment shows that bodies are sped in the same way also when they have different composition so the nuclear forces, the eletctrostatic energy of the atoms and the velocity of their electrons, even if they have different values according to the atom, doesn't affect the acceleration.-
Further exsperiments let him know that the distance covered by a body during his free fall is in proportion to the square of the time needed to cover it and let him deduce the equation of the motion of fall of bodies: r(t)=0.5gt2.
Also his studies on pendulums (that made him discover the proportion between the period of oscillation of a pendulum and the square of its length) could let him know the existence of g, but he tried to use them in order to create a clock. His projects about it were interrupted by his death in 1642.

According to the second principle of the dynamic, F=ma , the existence of an acceleration imply necessarily the existence of a force proportionated to it according to a constant called inertil mass.
For this reason also the acceleration of gravity had to be connected with a force, and it was Newton who made his efforts to the elaboration of a universal law of gravitation.
Among the contributions that this law brought there is the demonstration that the physical and the sublunar world obey the same laws, theory in great opposition to Aristotle's model which supposed deep and incompatible differences between the nature and the motion of the Earth and those of the celestial bodies. If Kepler confuted Aristotle's astronomical scheme with his laws on the kimatics of celestial bodies, Newton demonstred his fallacy also under the dynamic point of view.
The universal law of gravitation imply that each body in the Universe attracts the other even if sometimes the effects of this attraction are not visible because the presence of a massive body makes negligible the interactions between the others.
The predominance of one attraction on the others is due to the fact that the modulus of the gravitational force is
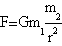
that means that every particle attract the other with a certrain intesity due to her mass. -In the equation G is the constant of universal gravitation, m1 and m2 are the interactive masses and r2 their distance.
Two men on the surface of the Earth are attracted the one by the other but the effects of that are invisible because the attraction of the Earth, according to her mass, is much bigger.In this case even if the men are distant just few metres their distance can be considered endless because the gravitational force they exerpt on eachother is null and given F as a fraction it is reasonable thinking that when the numerator is different from zero (the product between G and the masses is always positive) the fraction is null when the denominator tends to infinitive.
The existence of the gravitational attraction between any body is verifiable with the pendulum of torsion, tool used also by Cavendish who was the first who evalueted G.
The force of universal gravitation is also the force present in the interaction between the orbitating bodies and what is put in the focus of the ellipse they describe in their period of revolution (ex. between the Sun and the planets of the solar system).
The vector expression of the force of gravitation is
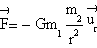
where ur is the radial vector directed from the focus of the ellipse to the orbitating body.
A limit of this theory stands in his author's inability of answering the objections moved by those, and first of all the bishop Berkley, who didn't understand how far and not communicating bodies could interact. Newton could never answer this critic and could just underline the effectiveness of his model which was better than everyone before.

The solution was found only at the beginning of the 20th century when Einstein elaborated his theory on the general relativity.
He interpreted the constance of the local acceleration of gravity, finally demonstred by the experiments done by Eötvos, as an intrinsic propriety of the physical space and supposed that masses, with their presence, curved it. For this reason he saw the attraction between two bodies as an effect of their motion in the space-time which was no longer seen as inert (as it had been always considered) and which was thought to obey laws different from those valid for the Euclidean geometry. (This is why, two parallel ways near a curvature of the space could converge).