Un vettore n-dimensionale è rappresentato da una lista di n elementi.
Due vettori di ugual dimensione possono essere sommati o sottratti tra di loro.
Esempio.
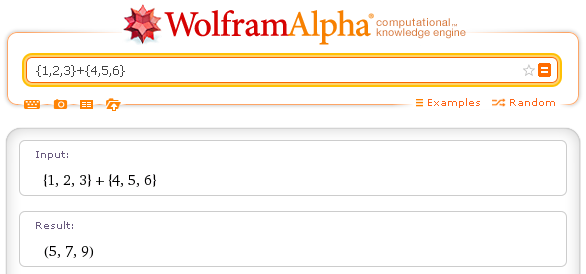
Somma di vettori tridimensionali: {1,2,3}+{4,5,6}

Un vettore può essere moltiplicato per uno scalare.
Esempio.
Scalare per vettore: Sqrt[2]*{Sqrt[2],Sqrt[8],Sqrt[32]}

Vettori di ugual dimensione possono essere moltiplicati scalarmente ottenendo un singolo valore numerico.
Il prodotto scalare si ottiene con l'operatore Dot (oppure con il semplice punto .).
Esempio.
Prodotto scalare di due vettori: Dot[{1,2,3,4},{5,6,7,8}]

Vettori di ugual dimensione possono essere moltiplicati vettorialmente ottenendo un vettore di dimensione uguale a quella dei fattori e ortogonale ai due fattori. Due vettori sono ortogonali se il loro prodotto scalare è 0. Il prodotto vettoriale si ottiene con l'operatore Cross.
Esempio.
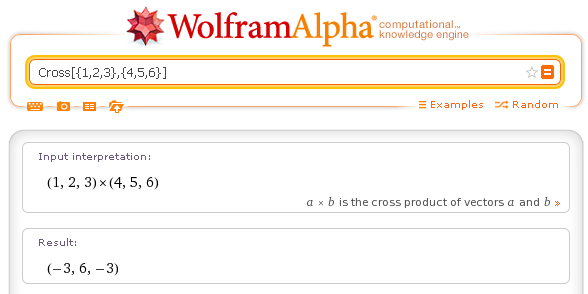
Prodotto vettoriale di due vettori: Cross[{1,2,3},{4,5,6}]
In questa sede ci si limita a considerare matrici quadrate. Una matrice quadrata di ordine n è una tabella di n righe ognuna composta da n elementi.
Una matrice in Mathematica è rappresentata da una lista di liste.
Esempio.
Matrice: {{1,2,3},{2,-1,4},{3,1,5}}

Usando l'operatore Dot (oppure il semplice punto .), si può moltiplicare una
matrice quadrata di ordine n per un vettore di ordine n ottenendo un vettore di ordine n.
Esempio.
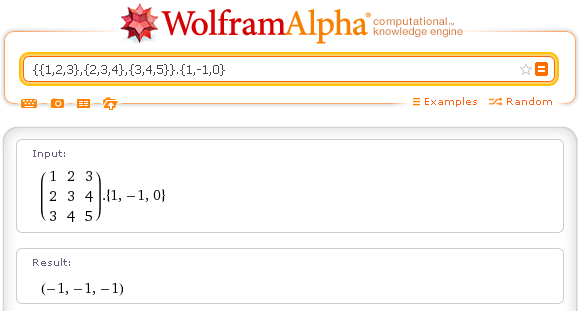
prodotto di matrice per vettore: {{1,2,3},{2,3,4},{3,4,5}}.{1,-1,0}
Due matrici quadrate dello stesso ordine possono essere sommate e moltiplicate tra loro.
Esempio.
prodotto di matrice per matrice: {{1,2,3},{2,3,4},{3,4,5}}.{{1,-1,0},{0,1,1},{1,1,0}}
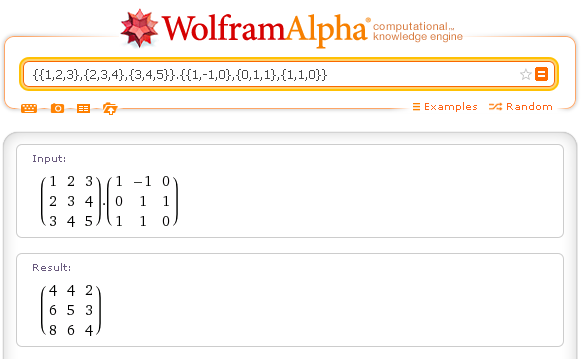
Il prodotto non è commutativo.
Esempio.
fattori invertiti: {{1,-1,0},{0,1,1},{1,1,0}}.{{1,2,3},{2,3,4},{3,4,5}}

Di una matrice si può calcolare il determinante con l'operatore Det.
Esempio.
Determinante: Det[{{1,2,3},{2,-1,4},{3,1,5}}]
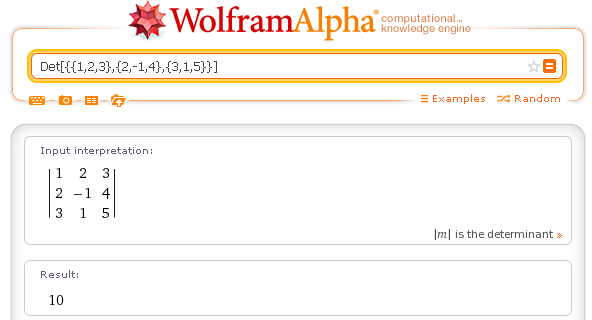
L'operatore Inverse produce la matrice inversa di una matrice con determinante non nullo.
Esempio.
Matrice inversa: Inverse[{{1,2,3},{2,-1,4},{3,1,5}}]

Il prodotto di una matrice per la sua inversa è la matrice neutra.
Esempio.
Determinante: Inverse[{{1,2,3},{2,-1,4},{3,1,5}}]
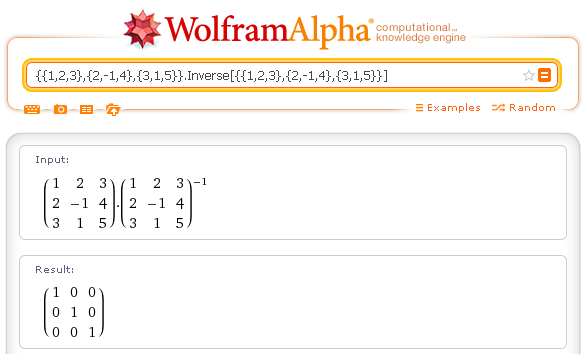
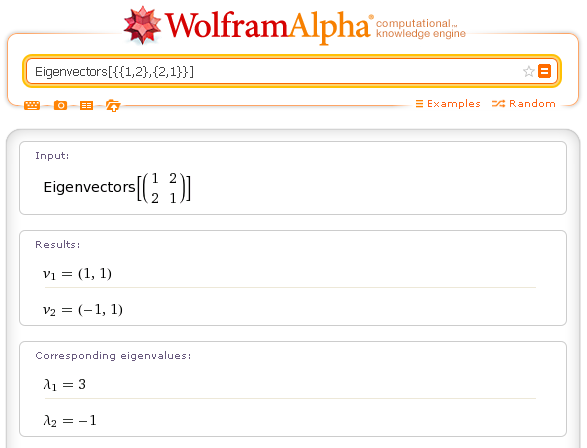
Di una matrice quadrata si possono ottenere autovalori e autovettori con gli operatori Eigenvalues e Eigenvectors.
Esempi.
Autovalori: Eigenvalues[{{1,2},{2,1}}]
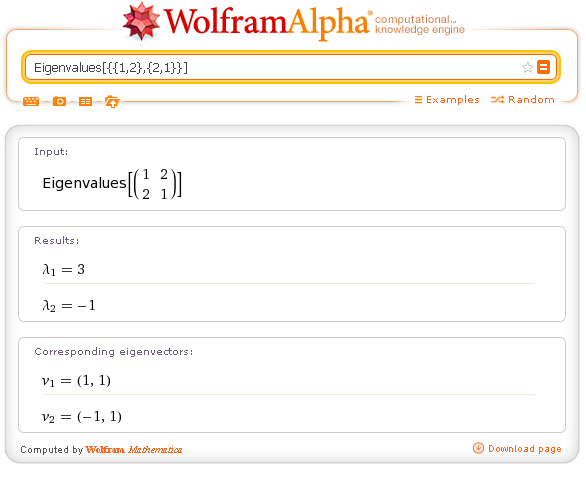
Autovettori: Eigenvectors[{{1,2},{2,1}}]