Dato un operatore lineare L definito sullo spazio vettoriale V, è spesso utile determinare l'insieme dei vettori di V per i quali l'applicazione dell'operatore equivale alla moltiplicazione per uno scalare.
I vettori di questo insieme sono detti autovettori (inglese: eigenvectors) li e gli scalari corrispondenti sono detti autovalori (inglese: eigenvalues) λi dell'operatore lineare L.
Per determinare autovettori e autovalori è necessario risolvere la seguente equazione (escludendo autovettori nulli) detta equazione agli autovalori
Questa equazione è equivalente a
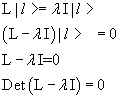
L'ultima equazione permette di calcolare gli autovalori λi e risulta in generale piuttosto impegnativa perché, sviluppata algebricamente, risulta di n-esimo grado e quindi, anche nel caso di matrici reali, può ammettere radici complesse.
La situazione più semplice si ha quando una matrice è diagonale,
cioè quando gli unici elementi non nulli sono quelli con indici uguali.
In questo caso l'equazione equivale all'annulamento di un prodotto di binomi
con l'ovvio insieme di soluzioni
.
Ogni autovalore li deve quindi verificare l'uguaglianza
Ciò è possibile solo se l'autovettore li ha tutte le componenti nulle tranne la i-esima.
Esempio.
Data la matrice diagonale
,
si ha
cioè
con soluzione
.
L'autovettore |d1>, corrispondente all'autovalore δ1=a,
si ottiene dall'equazione
,
cioè
,
vera per qualunque x se y=0. Il calcolo quindi non individua un preciso
vettore, ma l'insieme di tutti i vettori giacenti sull'asse delle ascisse. In sostanza
individua univocamente solo il versore dell'autovettore. È quindi sufficiente
limitarsi al calcolo di questi versori che saranno denominati autovalori normalizzati.
Nell'esempio proposto si assume quindi
.
Con un calcolo analogo relativo all'autovettore |d2>, corrispondente
all'autovalore δ2=2, si ottiene
.
|d1> e |d2> sono i versori degli assi cartesiani.
Le conclusioni ottenute nell'esempio si possono generalizzare a matrici diagonali n-dimensionali. Quindi, in generale,
Dall'equazione agli autovalori si deduce che, data la matrice L, una matrice M e la sua inversa M-1, la matrice M-1LM ha gli stessi autovalori di L. Infatti
Questo è vero in particolare per le rotazioni.
Se la matrice sottoposta alle rotazioni è una matrice reale diagonale, la matrice trasformata S è simmetrica, tale cioè che, per i≠j, Si,j=Sj,i. Infatti, limitandosi per semplicità al caso bidimensionale, si ha
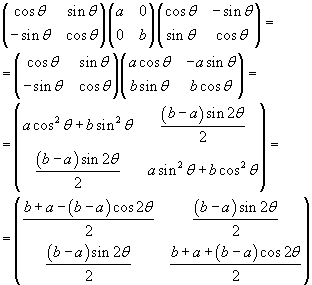
Viceversa, con una rotazione opposta si può ottenere da una matrice simmetrica una matrice diagonale.
Infatti, data la matrice
,
per individuare la rotazione che la diagonalizza, si pone
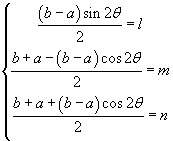
Sottraendo membro a membro la seconda equazione dalla terza si ha
Da questa equazione e dalla prima delle tre consegue
Quindi per diagonalizzare la matrice S, bisogna ruotare il sistema di un angolo -θ.
Questo metodo può essere esteso a matrici simmetriche di qualunque ordine. Quindi si può concludere che le matrici reali simmetriche ammettono autovalori tutti reali.
Esempio.
Calcolo di autovalori e autovettori della matrice simmetrica
.
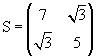Equazione agli autovalori:
.
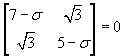Sviluppando il determinante si ha
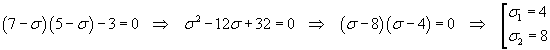
Gli autovalori sono σ1=4 e σ2=8. Per calcolare
gli autovettori normalizzati corrispondenti bisogna risolvere le equazioni
assumendo
che i vettori |si> abbiano modulo 1, cioè che possano essere espressi come
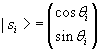con
.
Per il primo autovalore si ha
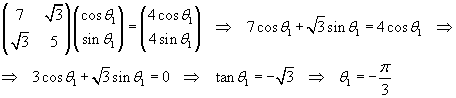
Quindi
.
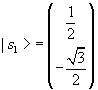Per il secondo autovalore si ha
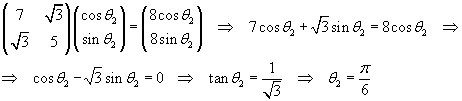
Quindi
.
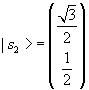Gli autovettori risultano ortogonali.
Con una rotazione la matrice S dell'esempio può essere trasformata nella matrice
diagonale con uguali autovalori
.
L'angolo di rotazione deve essere tale da far coincidere gli autovalori normalizzati di S
con i versori degli assi cartesiani. Nel caso proposto l'angolo è evidentemente π/6.
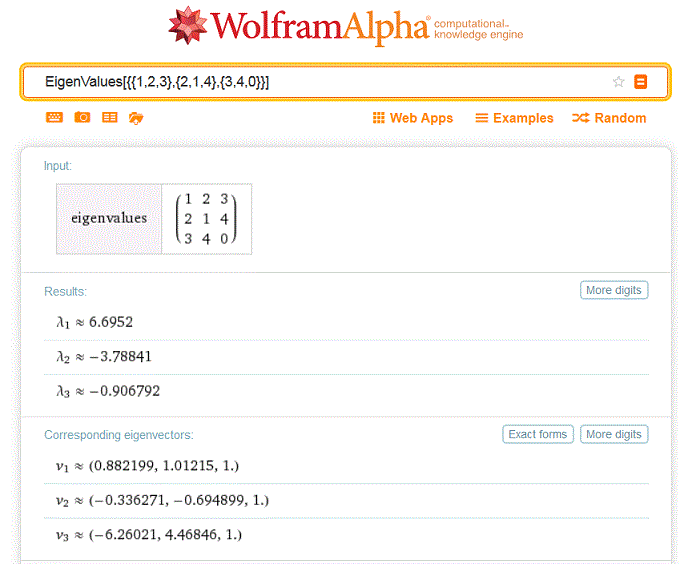
Calcolo di autovalori con WolframAlpha
