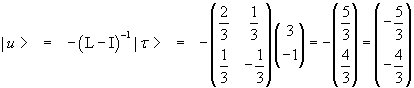Dato che traslazioni e trasformazioni lineari invertibili determinano corrispondenze biunivoche tra i punti di ℜ2, anche la composizione di una trasformazione lineare invertibile con una traslazione determina una corrispondenza biunivoca in ℜ2.
La composizione di una trasformazione lineare invertibile con una traslazione è detta trasformazione affine o affinità.
Una affinità può essere espressa algebricamente nel seguente modo
Si indica così che il vettore v'(x’;y’) biunivocamente corrispondente al
vettore v(x;y) si ottiene moltiplicando prima la matrice
per il vettore v e sottoponendo poi il risultato alla traslazione
τ(c;c’).
Esprimendo l'affinità in notazione matriciale si ha
L'affinità inversa esprime v in funzione di v’. Si ottiene
Le affinità mantengono tutte le proprietà delle trasformazioni lineari traslandone il centro.
Esempi.
Sia data l'affinità
Questa affinità è data dalla composizione della trasformazione lineare
con la
traslazione
Si ha Δ = - 3 e la matrice inversa risulta
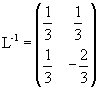
Si può quindi dire
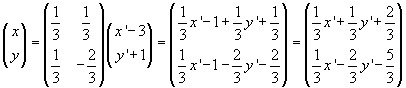
Tornando alla forma algebrica
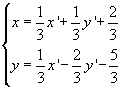
Data una trasformazione T si dicono punti uniti di T i vettori che corrispondono a sé stessi.
Un punto unito u di una affinità determinata da L e τ si determina risolvendo l'equazione
cioè
Nell'esempio proposto si ha
La matrice inversa di (L-I) risulta
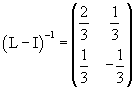
Moltiplicando l'opposto della matrice inversa per τ si ottiene l'elemento unito
