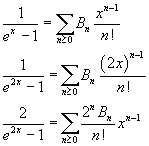
Sulla base dei risultati ottenuti nella sezione precedente si ha
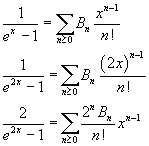
Usando la (3.9) per esprimere la cotangente iperbolica, si ottiene
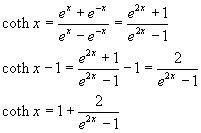
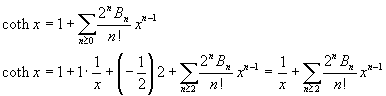
Se si scrivono esplicitamente alcuni addendi della somma si ha
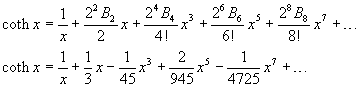
Infine, usando una notazione più compatta:
![]()
Lo sviluppo in serie della cotangente circolare può essere ottenuto dalle (9.1), (7.21) e (7.22)
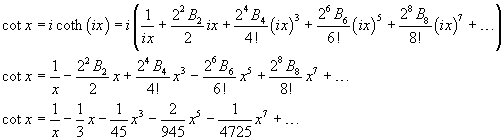
In modo più compatto:
![]()
Per ricavare lo sviluppo in serie della tangente iperbolica si può usare l'uguaglianza
![]()
Infatti
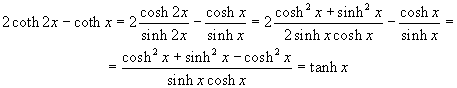
Quindi, applicando due volte lo sviluppo in serie della cotangente iperbolica, si ottiene
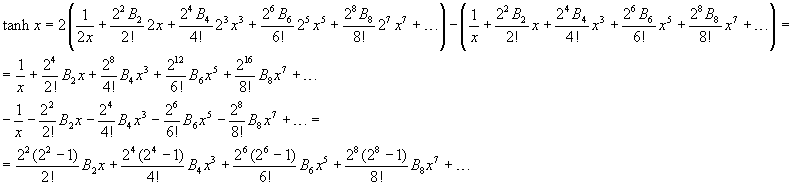
Calcolando esplicitamente i coefficienti, si ha
![]()
In modo più compatto:
![]()
Per ottenere lo sviluppo in serie della tangente circolare si può usare l'uguaglianza
![]()
Si ha
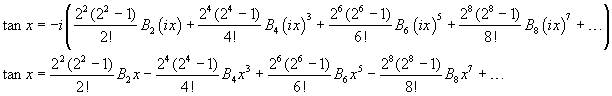
Calcolando esplicitamente i coefficienti, si ottiene
![]()
In modo più compatto:
![]()
Dato che
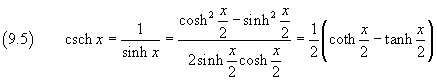
lo sviluppo in serie della cosecante iperbolica può essere ottenuto utilizzando gli sviluppi in serie della cotangente e tangente iperboliche. Dalle (9.1) e (9.3) si ha
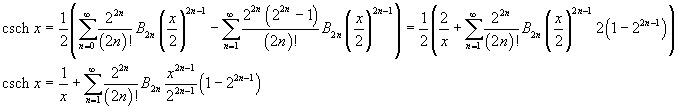
![]()
Esplicitando i coefficienti
![]()
Dalle (7.22) e (9.7) si ha
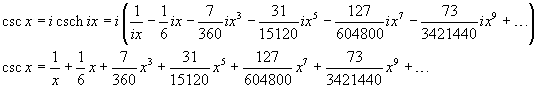
e, in modo più compatto,
![]()
La secante iperbolica può essere espressa in funzione dell'esponenziale
![]()
Questa espressione della secante iperbolica coincide con quella della funzione s(x) definita nella (8.2) della pagina precedente, quindi
![]()
dove En è lo n-esimo numero di Eulero. Dato che per indici dispari questi numeri sono nulli, si può più economicamente scrivere
![]()
Per le formule di Eulero la secante circolare è esprimibile come
![]()
Le potenze pari dell'unità immaginaria oscillano tra 1 e -1, quindi, in definitiva
![]()