Il seno iperbolico è una funzione definita su tutto R e sempre crescente: è dunque invertibile su tutto R. La sua funzione inversa è detta arcoseno iperbolico e si denota comunemente con arcsinh. Si ha
![]()
Dalla seconda delle (3.9), ricordando che ey>0, si ha
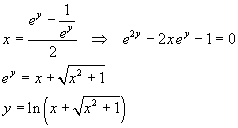
e infine
![]()
Dalla (6.1), appilcando la regola della derivazione a catena, si ottiene
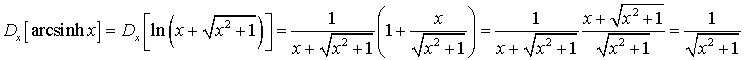
Il coseno iperbolico non è monotòno, dunque non si può invertire su tutto R. Per avere l'invertibilità bisogna restringere il suo dominio all'insieme dei reali non negativi. Solo in questo caso si può definire la sua funzione inversa, detta arcocoseno iperbolico e denotata da arccosh.
![]()
Dalla seconda delle (3.9), escludendo valori negativi di y,
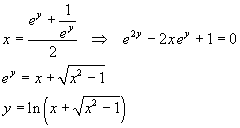
e infine
![]()
La (6.2) evidenzia che l'arcocoseno iperbolico è reale solo per argomenti ≥ 1.
Dalla (6.2), appilcando la regola della derivazione a catena, si ottiene
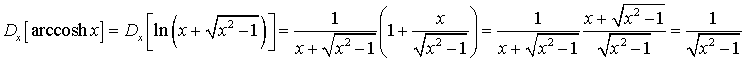
La tangente iperbolica è definita su tutto R ed è sempre crescente e quindi invertibile su tutto R. La sua funzione inversa, detta arcotangente iperbolica, è denotata comunemente da arctanh. Si ha
![]()
Dalla terza delle (3.9), ricordando che e2y>0, si ha
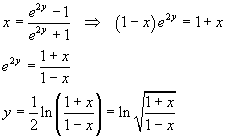
![]()
La (6.3) evidenzia che l'arcotangente iperbolica è reale solo per argomenti -1<x<1.
Dalla (6.3), appilcando la regola della derivazione a catena, si ottiene
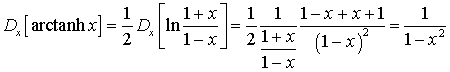
Note le derivate delle funzioni iperboliche inverse, č immediatamente possibile risalire alle antiderivate delle derivate, cioč ottenere gli integrali indefiniti delle derivate.
![]()
![]()
![]()
Integrando per parti si ha:
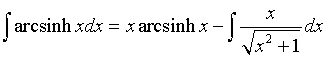
Nell'integrale sottraendo del secondo membro la funzione integranda è evidentemente la derivata di ![]() , dunque
, dunque
![]()
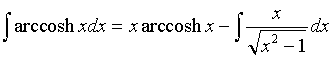
Nell'integrale sottraendo del secondo membro la funzione integranda è evidentemente la derivata di ![]() , dunque
, dunque
![]()

Nell'integrale sottraendo del secondo membro la funzione integranda è evidentemente la derivata di 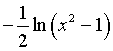 , dunque
, dunque
