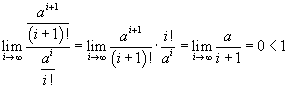Se ![]() e
e
![]() sono due serie di numeri reali
tali che, per qualunque i, 0 ≤ ai ≤ bi, allora
sono due serie di numeri reali
tali che, per qualunque i, 0 ≤ ai ≤ bi, allora
Dimostrazione.
Esempio.
La serie ![]() (Serie di Mengoli)
è convergente. Infatti
(Serie di Mengoli)
è convergente. Infatti
![]()
Allora anche la serie 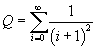 è convergente
perché gli elementi del suo resto di ordine 1,
è convergente
perché gli elementi del suo resto di ordine 1,
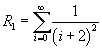 , sono maggiorati dagli elementi di M
di uguale indice. Per il teorema del confronto
questo resto converge e di conseguenza converge la serie Q.
, sono maggiorati dagli elementi di M
di uguale indice. Per il teorema del confronto
questo resto converge e di conseguenza converge la serie Q.
Se ![]() è una successione di numeri reali
positivi tale che
è una successione di numeri reali
positivi tale che ![]() (con α ovviamente non negativo ma diverso da 1), allora la serie
(con α ovviamente non negativo ma diverso da 1), allora la serie
![]() :
:
Dimostrazione.
Dall'ipotesi segue che per qualunque ε reale positivo esiste un indice k tale che, per ogni
m>k, 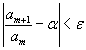
Se α<1, si può assumere in particolare
![]() e quindi
e quindi 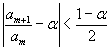 , da cui
, da cui
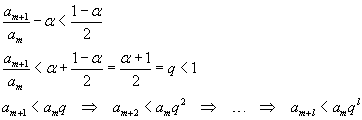
I termini maggioranti sono in successione geometrica. La loro serie, per q< 1, converge e quindi, per il teorema del confronto, converge anche il resto m-esimo della serie A e, in definitiva, la stessa serie A.
Se α>1, si può assumere in particolare
![]() quindi
quindi
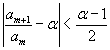 da cui
da cui
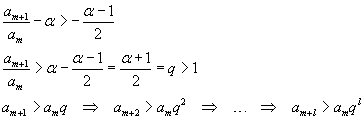
I termini minoranti sono in successione geometrica. La loro serie, per q> 1, diverge e quindi, per il teorema del confronto, diverge anche il resto m-esimo della serie A e, in definitiva, la stessa serie A.
Esempio.
La serie ![]() converge per ogni
a reale positivo. Infatti
converge per ogni
a reale positivo. Infatti