Una successione si dice limitata se esiste un numero reale positivo M tale che, per ogni indice
i,
![]() .
.
In caso contrario la successione è detta divergente.
Per indicare che una successione diverge positivamente, cioè che è tale che, comunque si fissi un M positivo, da un certo indice i in poi, tutti gli ai superano M, si dice che il limite della successione per i che tende all'infinito è +∞ e si scrive
![]()
Viceversa, per indicare che una successione diverge negativamente, cioè che è tale che, comunque si fissi un M positivo, da un certo indice i in poi, tutti gli ai risultano minori di -M, si dice che il limite della successione per i che tende all'infinito è -∞ e si scrive
![]()
Il simbolo ∞ (aleph) non è un numero reale: è solo un ideogramma usato per rappresentare la divergenza della successione.
Si possono definire successioni divergenti che non ricadono in nessuna delle due categorie precedenti.
Esempi.
![]()
La successione dei numeri naturali diverge positivamente.
![]()
La successione degli opposti dei numeri naturali diverge negativamente.
![]()
Non esiste.
Se una successione {ai} è limitata e se esiste un numero reale a tale che, al crescere dell'indice i, la distanza degli ai da a va sempre diminuendo, si dice che la successione converge ad a, o in modo del tutto equivalente, che la successione ha limite (o tende ad) a e si scrive
![]()
In modo più formale, si dice che la successione {ai} tende ad a se fissato un numero reale positivo ε comunque piccolo, esiste un indice j (dipendente da ε e tanto più grande quanto più ε è piccolo) tale che
![]()
Esempio: se q è un numero di modulo minore di 1 e diverso da 0, la successione delle potenze di q converge a 0.
Bisogna dimostrare che ![]() se i
supera un certo valore j.
se i
supera un certo valore j.
Se q è positivo
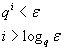
Se q=0.5 e ε=0.001 si ha i>9, quindi per ogni esponente maggiore di 9 le potenze di 0.5 sono minori di 0.001.
Se invece ε=0.0001 si ha i>13, quindi per ogni esponente maggiore di 13 le potenze di 0.5 sono minori di 0.0001.
Se q è negativo
![]()
e si è ricondotti al caso precedente.
Se una successione converge, il limite è unico.
Se si ammette che esistano due limiti diversi a e a* si ha
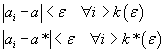
Per ogni i maggiore del maggiore tra k e k* si ha
![]()
Per la disuguaglianza triangolare la somma di due moduli è maggiore o al minimo uguale al modulo della differenza dei loro argomenti, dunque
![]()
Dato che ε può essere piccolo a piacere, a e a* devono coincidere. Dunque è assurdo ammettere che possano esistere due limiti diversi.
Se una successione è convergente, allora, al crescere dell'indice, la distanza tra due elementi va diminuendo.
Per esprimere lo stesso concetto in modo più formale: se una successione è convergente, allora, fissato un numero reale positivo ε comunque piccolo, esiste un indice k (dipendente da ε e tanto più grande quanto più ε è piccolo) tale che per qualunque coppia di indici i e j successivi a k
![]()
Dimostrazione. Per ipotesi, detto a il limite della successione, per i e j entrambi maggiori di un certo k si ha
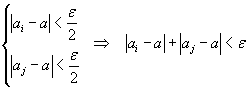
Inoltre
![]()
Si è applicata la disuguaglianza triangolare per cui il modulo di una somma è minore o al massimo uguale alla somma dei moduli. Quindi, in definitiva,
![]()
La successioni che godono di questa proprietà si chiamano successioni di Cauchy dal nome del matematico francese A. L. Cauchy.
Quindi se una successione converge allora è una successione di Cauchy.
Si può, viceversa, dimostrare che, se una successione è una successione di Cauchy, allora converge.
Si supponga che la successione {ai} sia una successione di Cauchy e si considerino due elementi
di indici i e j tali che, in corrispondenza di un ε prefissato,
![]() .
.
Non si può ammettere che per qualunque a reale
![]()
perché con a=ai o a=aj l'ammissione è contraddittoria. Dunque esiste almeno un a tale che
![]()
Perché una somma di numeri non negativi sia minore di ε bisogna che entrambi gli addendi siano minori di ε. Quindi
![]()
cioè la successione {ai} converge ad almeno una a ma, per l'unicità del limite, questa a è unica.
Si può quindi affermare che condizione necessaria e sufficiente perché una successione sia convergente è che sia una successione di Cauchy.