Una proprietà di un sistema fisico, biologico o sociale può in generale assumere diversi valori qualitativi o quantitativi.
Ad esempio, il sesso di un essere umano può essere maschile o femminile, e il suo stadio di sviluppo può essere l'infanzia, l'adolescenza, la giovinezza, la maturità e la vecchiaia. Un essere umano è caratterizzato inoltre da età e altezza di norma specificate da numeri. Sesso stadio di sviluppo sono caratteri qualitativi. Età e altezza sono caratteri quantitativi.
L'insieme dei valori, che può essere discreto o continuo, che possono essere assunti da una o più proprietà di un sistema, è detto spazio campione o, più semplicemente campione, S.
Ogni sottinsieme Ex di S è detto evento o esperimento.
Una funzione reale p(Ex) tale che, dato
![]() ,
,
![]()
![]()
![]()
![]()
![]()
è detta funzione di probabilità.
Per esempio, lo spazio campione delle uscite del lancio di un dado è S={1,2,3,4,5,6}.
Gli eventi sono suoi sottinsieme come E1 = {1}, E2 = {2}, E3 = {3}, E4 = {4}, E5 = {5}, E6 = {6}, E12 = {1,2}, E246 = {2,4,6}, ecc.
L'uguaglianza (2.4) dà
![]()
quindi, se
![]() , si ottiene
, si ottiene
![]()
Si ha inoltre
![]()
![]()
![]()
Se uno spazio campione S è il prodotto cartesiano
di due altri campioni Sx e Sy e
![]() , il simbolo
, il simbolo
![]() (la probabilità di
Ey dato Ex) rappresenta la probabilità dell'evento
(la probabilità di
Ey dato Ex) rappresenta la probabilità dell'evento
![]() .
E è detto evento composto.
.
E è detto evento composto.
Se ![]() , gli eventi
Ex e Ey sono detti mutualmente indipendenti,
o, più semplicemente, indipendenti; altrimenti essi sono dipendenti.
, gli eventi
Ex e Ey sono detti mutualmente indipendenti,
o, più semplicemente, indipendenti; altrimenti essi sono dipendenti.
Se, per esempio, una scatola contiene tre palle, una rossa, una verde e una blu, ed estraiamo una palla a caso,
la probabilità p(R) di estrarre una palla rossa è
![]() .
.
Se facciamo due estrazioni consecutive Ex e Ey, abbiamo un evento composto diverso a seconda che, dopo la prima estrazione, rimettiamo o no nell'urna la palla estratta.
Nel primo caso lo spazio campione è
![]() .
.
Ci sono tre casi su nove in cui la seconda palla estratta è rossa, quindi
![]() . In questo caso la probabilità
che la seconda palla sia rossa è uguale alla probabilità
p(Ey)=p(R) di estrarre una palla rossa in una singola estrazione:
gli eventi Ex and Ey sono indipendenti.
. In questo caso la probabilità
che la seconda palla sia rossa è uguale alla probabilità
p(Ey)=p(R) di estrarre una palla rossa in una singola estrazione:
gli eventi Ex and Ey sono indipendenti.
Nel secondo caso lo spazio campione è
![]() e, come è ovvio, la seconda palla
non può essere rossa: p(Ey|Ex)=0≠p(Ey).
e, come è ovvio, la seconda palla
non può essere rossa: p(Ey|Ex)=0≠p(Ey).
Gli eventi Ex e Ey sono dipendenti.
In generale, se ![]() è un evento
composto,
è un evento
composto,
![]()
In particolare:
se Ex e Ey sono indipendenti,
![]()
se ![]()
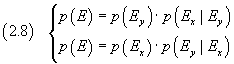
Qual è la probabilità che in un gruppo di n persone scelte a caso, due di esse abbiano lo stesso compleanno?
Sia p(n) la probabilità richiesta. La soluzione risulta più agevole se prima si calcola la probabilità opposta
![]() .
Per semplicità non si considerano gli anni bisestili e si assumono le nascite uniformemente distribuite nel corso
dell'anno.
.
Per semplicità non si considerano gli anni bisestili e si assumono le nascite uniformemente distribuite nel corso
dell'anno.
Per esempio, la probabilità che su 80 persone ce ne siano due con lo stesso compleanno è
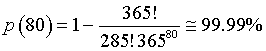 :
è praticamente sicuro che ci siano due persone con lo stesso compleanno.
:
è praticamente sicuro che ci siano due persone con lo stesso compleanno.
Avremmo potuto ottenere lo stesso risultato con il calcolo combinatorio. Infatti q(n) è dato dal rapporto tra le combinazioni C365,n (cioè tutti i possibili gruppi di n compleanni) e le permutazioni con ripetizione P365,n, notando che le permutazioni degli stessi elementi sono indistinguibili e vanno contate una sola volta.
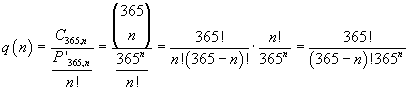
Prove bernoulliane
Siano S lo spazio campione dei possibili risultati di una prova e
![]() due eventi tali che
due eventi tali che
![]() .
.
Se e un possibile risultato, qual è la probabilità che in n repliche della stessa prova,
![]() k volte?
k volte?
Si assume che gli esiti delle prove siano indipendenti l'uno dall'altro e, per semplicità, si pone
![]() di modo che
di modo che
![]() .
.
q è detta probabilità opposta rispetto a p.
La probabilità che
![]() in k
esperimenti e che
in k
esperimenti e che
![]() nei rimanenti n-k
esperimenti è
nei rimanenti n-k
esperimenti è
![]() .
.
Dato che questa combinazione può avere
![]() permutazioni, la probabilità richiesta è
permutazioni, la probabilità richiesta è
![]()
Esempi.
Se se lancia un dado dieci volte, qual è la probabilità di ottenere 1 due volte?
La probabilità di ottenere 1 in una singolo lancio è
![]() , quindi
, quindi
![]() . Dalla (2.9) si ottiene
. Dalla (2.9) si ottiene
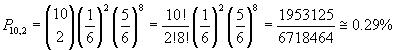
Qual è la probabilità di ottenere 1 almeno una volta?
Conviene calcolare la probabilità che non esca mai 1:
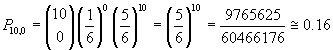
e quindi calcolare la probabilità opposta
![]()
Nella seguente applicazione JS la probabilità p può essere espressa come decimale o come frazione.
Teorema di Bayes
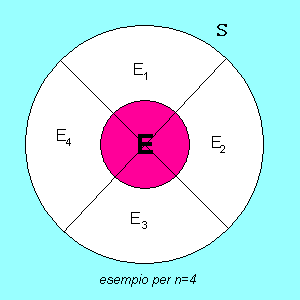
Sia S lo spazio campione di un esperimento e siano Ek (k da 1 a n) eventi di S tali che
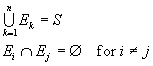
Dato un qualsiasi evento E di S, si ha
![]()
Dalla (2.4) si ha
![]()
e dalla (2.5)
![]()
La (2.12) è uno dei possibili modi di esprimere il teorema di Bayes.
Esempio.
In una scuola ci sono 600 ragazze e 400 ragazzi. Il 40% delle ragazze e il 30% dei ragazzi hanno buoni voti in matematica. Qual è la probabilità che una persona che studia in quella scuola sia brava in matematica?
Siano p(E) la probabilità richiesta, p(E1) la probabilità che la persona sia femmina, p(E2) la probabilità che la persona sia maschio, p(E|E1) la probabilità che una ragazza abbia buoni voti e p(E|E2) la stessa probabilità per un ragazzo.
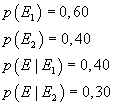
Dalla (2.12) si ottiene
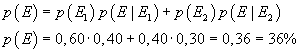
Lo stesso calcolo può essere svolto in modo più elementare:
Dalla (2.8) si ottiene
![]()
Se in questa uguaglianza si pone
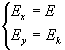
si ha
![]()
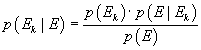
e infine
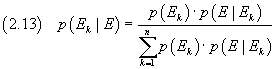
L'uguaglianza (2.13) è un altro possibile modo di esprimere il teorema di Bayes.
Nell'esempio precedente, qual è la probabilità che chi ha buoni voti sia una ragazza?
Dalla (2.13) si ha
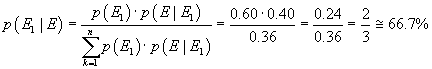
In modo più elementare: