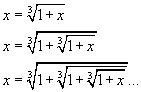
Ricercando metodi analoghi a quelli usati nella determinazione del numero aureo Φ, si possono individuare successioni di numeri reali o razionali che convergano a P.
Ad esempio, si può scrivere l'equazione nella forma
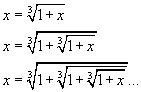
e definire la successione
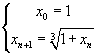
Con una calcolatrice tascabile si ottengono i seguenti valori approssimati
| 1.0 |
| 1.259921049894873 |
| 1.3122938366832888 |
| 1.3223538191388249 |
| 1.324268744551578 |
| 1.3246326252509202 |
| 1.3247017485103587 |
| 1.3247148784409506 |
| 1.324717372435671 |
| 1.3247178461621454 |
| 1.324717936144965 |
Volendo ottenere successioni di termini razionali si possono usare diverse metodologie.
Scrivendo l'equazione plastica nella forma equivalente
si può definire la successione
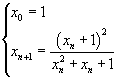
cioè
| frazione | approssimazione decimale |
|---|---|
| 1 | 1.0 |
| 4 / 3 | 1.33333333333333333333... |
| 49 / 37 | 1.3243243243243243243... |
| 7396 / 5583 | 1.3247358051226938922... |
| 168454441 / 127162573 | 1.3247171477098060921 |
Applicando il metodo della tangente alla ricerca dello zero reale della funzione
si definisce la successione
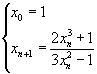
cioè
| frazione | approssimazione decimale |
|---|---|
| 1 | 1.0 |
| 3 / 2 | 1.5 |
| 31 / 23 | 1.3478260869565217391... |
| 71749 / 54142 | 1.32520039895090687451... |
| 448712783118393 / 338723203112569 | 1.3247181739990537344... |