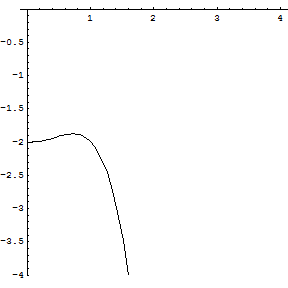
Funzione:
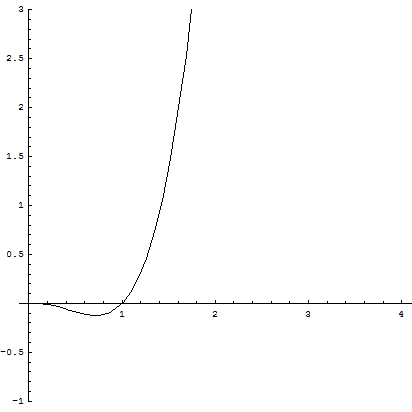
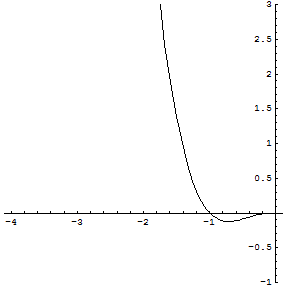
Nel dominio, la funzione ha il segno del logaritmo, quindi è negativa per x<1, positiva per x>1 e interseca l'asse x nel punto di ascissa 1.
Per il calcolo del limite per x→0, conviene applicare la regola di De L'Hôpital:
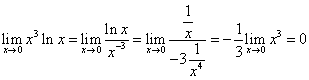
La derivata prima è 
ed è positiva per
La f decresce in 
, cresce in
e ha in minimo relativo di coordinate
.
La derivata seconda è 
ed è positiva per
La funzione ha concavità negativa in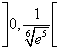 
,
positiva in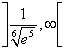 
e un flesso di coordinate
.
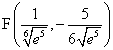I valori approssimati delle ascisse sono 0.717 e 0.435.
La parabola richiesta ha equazione di forma 
. Il passaggio per
l'origine impone c=0 e il passaggio per P(1;0) impone 
In definitiva l'equazione della parabola ha forma 
.
Per x=1 la sua derivata prima deve coincidere con la derivata di γ. Si ha quindi
e l'equazione richiesta è
.
L'area richiesta è data da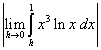 
.
L'integrale indefinito si può calcolare per parti:
Questo integrale, per x=1 vale 
.
Inoltre
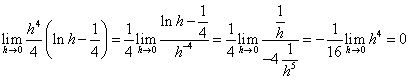
L'area richiesta risulta quindi 
Le equazioni di una simmetria assiale rispetto all'asse delle ordinate sono
quindi la curva simmetrica di γ rispetto all'asse y ha equazione 
.
Le equazioni di una simmetria assiale rispetto alla retta y=-1 sono
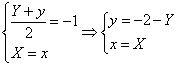
quindi la curva simmetrica di γ rispetto alla retta y=-1 ha equazione 
.
