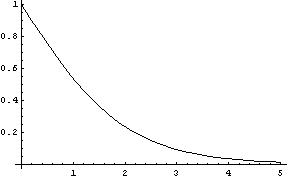
Per x→∞,il primo addendo diverge positivamente, il secondo è costante, il terzo tende a 0. Il limite è +∞.
Per x→-∞,il primo addendo diverge negativamente, il secondo è costante, il terzo tende a 2. Il limite è -∞.
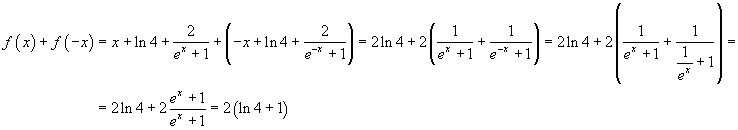
Considerato il segmento delimitato da due punti di Γ aventi ascisse opposte, il punto
è il punto medio di tale segmento.
Dunque la curva ha una simmetria centrale di centro C.
Considerata la funzione
si ha
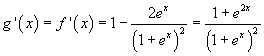
g'(x) è evidentemente sempre positiva, quindi g(x) è sempre crescente e, dato che g(x) come f(x) è continua su tutto R e ha codominio R, per il teorema di continuità di Bolzano, si azzera una e una sola volta, cioè l'equazione assegnata ammette una e una sola soluzione.
Si ha
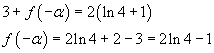
Dunque il valore di m richiesto è
Per dimostrare che le due espressioni della f(x) sono identiche basta dimostrare che la loro differenza è identicamente nulla.
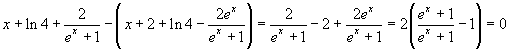
Per il calcolo degli asintoti si ha
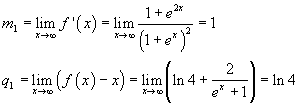
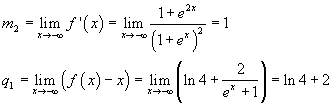
Bisogna dimostrare che per ogni x
La prima disuguaglianza
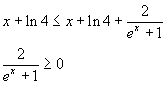
è evidente, in quanto numeratore e denominatore della frazione sono sempre positivi. La seconda disuguaglianza
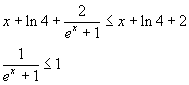
è essa pure immediata, in quanto il denominatore è sempre maggiore di 1.
L'integrale proposto è
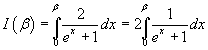
L'integrale può essere calcolato nel seguente modo
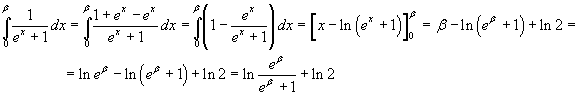
Da cui
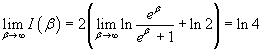
Il valore ricavato può essere interpretato geometricamente come l'area compresa tra la curva di equazione
, l'asse delle ascisse e l'asse
delle ordinate.
