Perché la funzione soddisfi alle condizioni imposte è necessario che
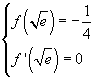
Derivando si ha
![]()
Si ottiene quindi
![]()
Si ha in definitiva
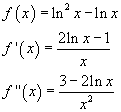
Per controllare che nel punto indicato ci sia un minimo si calcola il segno della derivata seconda che deve essere positivo:
![]()
f ( x ) è reale solo per argomenti positivi ed è continua e derivabile in tutto il suo dominio.
L'insieme di positività si ottiene risolvendo la disequazione
![]()
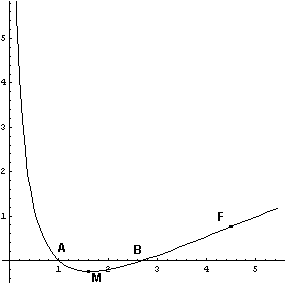
La funzione è positiva in ] 0 ; 1 [ U ] e; ∞ [, negativa in ] 1 ; e [. Il grafico interseca l'asse delle ascisse nei punti A ( 1 ; 0 ) e B ( e ; 0 )
Per x tendente a 0 e per x tendente a infinito la funzione diverge.
La derivata prima
![]()
nel dominio è positiva dove è positivo il numeratore
![]()
La funzione è decrescente in ] 0 ; √e[, crescente in ] √e ; ∞ [ e ha un minimo relativo e assoluto nel punto assegnato.
La derivata seconda
![]()
è positiva dove è positivo il numeratore
![]()
La funzione ha concavità verso l'alto in ] 0 ; e√e[, verso il basso in ] e√e ; ∞ [
e ha un flesso obliquo nel punto
F ( e√e ; 3/4 ).
L'area richiesta si ottiene calcolando il valore assoluto dell'integrale di f ( x ) da 1 a e.
A questo scopo si può effettuare un cambio di variabile:
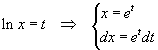
Nella variabile t l'integrale da calcolare risulta quindi
![]()
Il valore può essere ottenuto integrando ripetutamente per parti
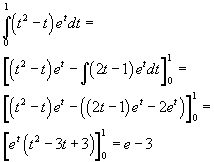
L'area chiesta è quindi 3 - e.
La probabilità che in un lancio di dado esca un numero predeterminato è
![]()
La probabilità che su cinque lanci esca per tre volte un numero predeterminato è, per il teorema delle prove ripetute,
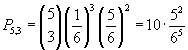
La probabilità che su cinque lanci esca per tre volte un numero qualunque dei sei possibili è
![]()