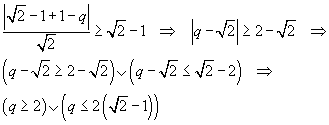Il semiperimetro del triangolo OAB è
![]()
Considerando il lato OA a l'angolo retto opposto OBC si ha, per una nota relazione trigonometrica, che il raggio r della circonferenza inscritta è
![]()
L'incentro appartiene a tutte le bisettrici degli angoli interni, in particolare alla
bisettrice dell'angolo OBA, che è evidentemente la retta di equazione y = 1.
L'ordinata dell'incentro è quindi 1. La circonferenza inscritta deve essere tangente
all'asse delle ordinate, quindi l'ascissa dell'incentro coincide con la misura del raggio.
L'incentro I è quindi
![]()
L'equazione della circonferenza inscritta risulta quindi
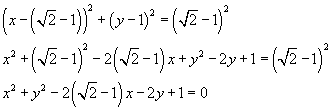
In generale, le equazioni di un' affinità sono di tipo
![]()
L'origine viene trasformata in se stessa, dunque l'affinità è una trasformazione lineare
![]()
C ( 1 ; 0 ) si trasforma in se stesso, quindi
![]()
per cui
![]()
Infine, B ( 1 ; 1 ) si trasforma in A ( 0 ; 2 )
![]()
Le equazioni di α sono quindi
![]()
Applicando α alle coordinate di A ( 0 ; 2 ) si ottiene A ' ( -2 ; 4 ).
L'area del triangolo CAA' è data da
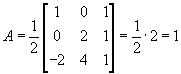
I punti uniti di α si trovano risolvendo il sistema
![]()
vero per qualunque punto dell'asse delle ascisse. Quindi tutti i punti dell'asse delle ascisse sono punti uniti di α. Ovviamente l'asse delle ascisse è una retta unita.
Una retta unita r: y = m x + q si trasforma in se stessa. Per determinare i parametri m e q si calcola la sua trasformata e si impone che i suoi parametri m' e q' coincidano rispettivamente con m e q. Deducendo x e y in funzione di X e Y si ha
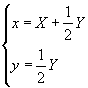
La trasformata di r risulta quindi
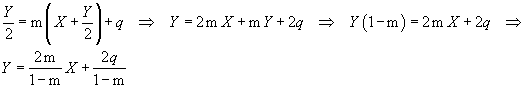
Uguagliando i coefficienti, per il principio di identità dei polinomi,
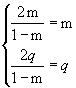
Le soluzioni del sistema sono
![]()
La prima soluzione fa ritrovare l'asse delle ascisse, già individuato.
Dalla seconda si desume che tutte le rette del fascio f: y = - x + q sono rette unite.
Ovviamente l'asse delle ascisse è esterno alla circonferenza γ.
Le rette del fascio f sono tangenti o esterne a γ se la loro distanza dal centro I non è minore del raggio r