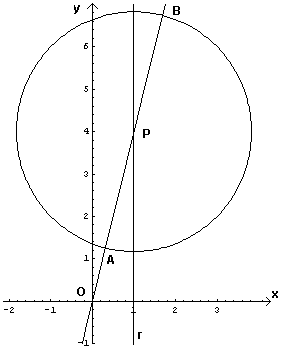
(a cura di Roberto Bigoni)
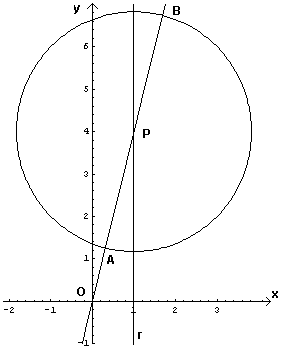
Detta m l'ordinata di P, la retta OP ha equazione y = m x e la circonferenza
![]()
I luoghi dei punti A e B determinano eliminando il parametro m dal sistema
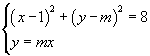
Sviluppando l'equazione risolvente
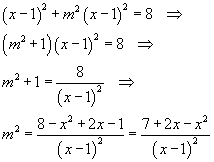
Sostituendo i due possibili valori di m nell'equazione della retta OP si ha
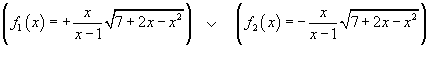
![]()
f1 ( x ) non esiste dove si annulla il
denominatore e non è reale dove il radicando è
negativo.
Gli zeri del radicando sono 1 ± 2√ 2. Il dominio
di realtà di f1 ( x ) è dunque
![]()
Il radicale, nel dominio, è non negativo e si annulla negli zeri del radicando che determinano punti d'arresto per la funzione. La frazione x/(x-1) è positiva per x negativi o maggiori di 1, nulla per x nullo, negativa per x positivi minori di 1.
In definitiva la f1 ( x )
Per x = 1, f1 ( x ) ha una singolarità di seconda specie e il grafico presenta un asintoto verticale.
Derivando f1 ( x ) con le usuali regole si ottiene
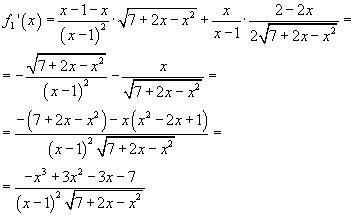
Si osserva subito che f1 ( x ) non è derivabile, oltre che nella singolarità, anche agli estremi del dominio: in questi punti il grafico ha tangente verticale.
Il segno di f1' ( x ) coincide con il segno del numeratore. Si osserva inoltre che il numeratore si annulla per x = -1 e quindi, per il teorema del resto, è divisibile per x + 1. Eseguendo la divisione si ha
![]()
Dato che il trinomio di secondo grado ha discriminante negativo, esso è negativo in tutto il dominio: f1' ( x ) è positiva dove x + 1 è negativo, cioè per x < -1.
In definitiva, f1 ( x )
La γ2 è simmetrica di γ1 rispetto all'asse delle ascisse.
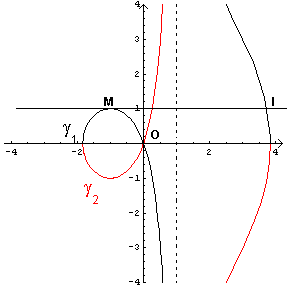
Il massimo relativo M ha coordinate M ( -1 ; 1). f1' ( -1 ) = 0 quindi la tangente al massimo è la retta di equazione t: y = 1. L'ulteriore punto di intersezione tra questa retta e γ1 si trova risolvendo il sistema
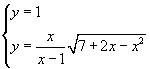
nel dominio E sapendo inoltre che ci sono due soluzioni coincidenti per x = -1.
L'equazione risolvente è
![]()
Per x > 1 si ha
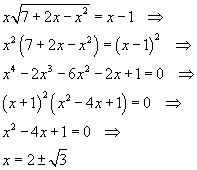
L'unica soluzione accettabile è x = 2 + √3.
Calcolando la funzione per questo argomento si ha 1.
Risulta quindi I ( 2 + √3 ; 1 ).
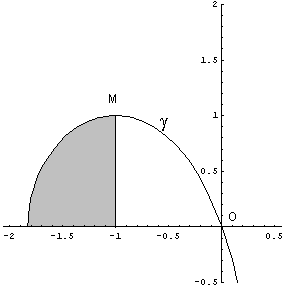
Per l'approssimazione del valore dell'integrale richiesto si può applicare il metodo dei trapezi: graficamente, si calcola il sottomultiplo ennesimo Δx = ( b - a ) / n dell'intervallo di integrazione, si tracciano per i punti a, a+Δx, a+2Δx,... dell'asse delle ascisse le parallele all'asse delle ordinate e si uniscono con segmenti le intersezioni di queste rette con la curva, costruendo un poligono, formato da una somma di trapezi, la cui area approssima per difetto quella sottesa dalla curva. L'approssimazione sarà tanto migliore quanto maggiore è n.
Come esempio di programmazione si propone il codice Javascript (facilmente adattabile anche al C) usato nella form seguente. La funzione appr_integrale(n) viene invocata passandole come parametro la potenza di 10 il cui reciproco indica l'ordine di grandezza dell'approssimazione.
function f(x)
{
return x/(x-1)*Math.sqrt(7+2*x-x*x);
}
function appr_integrale(n)
{
eps = Math.pow(10,-n);
result = 0;
a = 1-2*Math.sqrt(2);
b = -1;
cost = 0.5*f(b);
k = 0;
do
{
prec = result;
k +=100;
dx = (b-a)/k;
result = cost;
x = a;
for (i=1; i<k; i++)
{
x += dx;
result += f(x);
}
result *= dx;
} while (Math.abs(result-prec) ≥ eps);
return result;
}
![]()