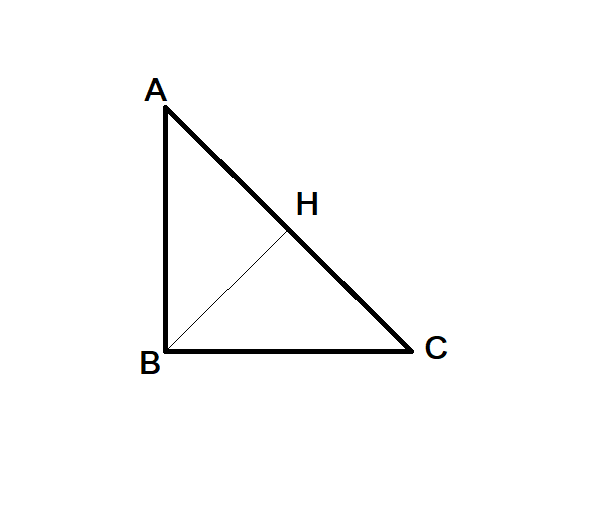
La condizione è sufficiente. Infatti dato il triangolo rettangolo ABC di ipotenusa AC e detta H la proiezione del vertice B su AC,
se la misura di BH è h e la misura di AC è 2h, il triangolo ABC è
scomponibile in due triangoli rettangoli congruenti con ipotenuse coincidenti con i cateti di ABC, quindi ABC è isoscele.
La condizione è necessaria. Infatti se un triangolo ABC è rettangolo e isoscele, allora l'altezza BH lo divide in due triangoli rettangoli e isosceli
ABH di cateti BH e AH e CBH di cateti BH e CH e la misura di AC risulta doppia della misura di BH.
La probabilità che un evento di probabilità p si presente k volte in una serie di n prove è
.
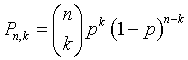Nel caso proposto si ha quindi
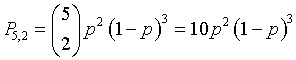
Per ipotesi 0<p<1 quindi l'espressione ottenuta è sempre positiva ed è minima dove la sua derivata si annulla.
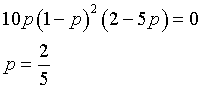
Dati il piano Π di equazione ax+by+cz+d=0 e il punto P(xP;yP;zP), la proiezione H di P su Π è
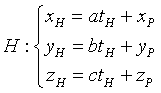
con
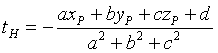
Nel nostro caso si ha tH = -1 e quindi H(1,4,1)
L'intersezione dell retta s con Π è data dalla soluzione del sistema
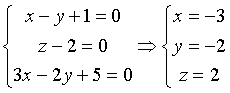
Gli zeri della funzione 
sono le soluzioni del sistema
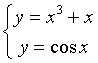
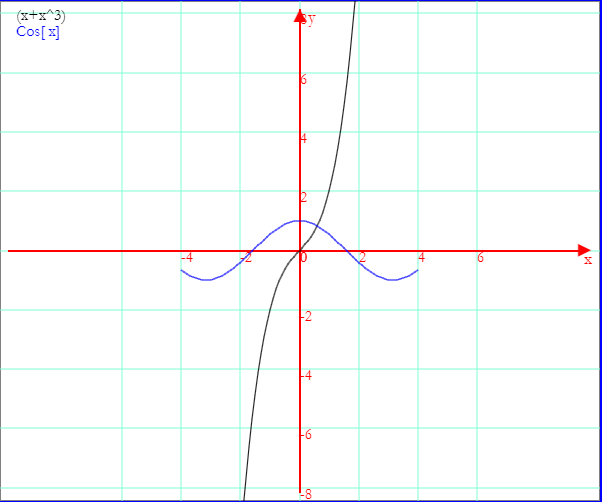
La funzione algebrica, definita e continua ∀x, ha derivata prima y'=3x2+1 sempre positiva dunque è sempre crescente e il suo codominio è ℜ.
La funzione trigonometrica è definita e continua ∀x ma il suo codominio è [-1,1].
La graficazione delle due funzioni evidenzia una unica intersezione tra i loro grafici e quindi una unica soluzione reale dell'equazione.
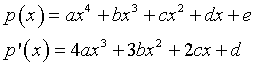
Le condizioni imposte implicano
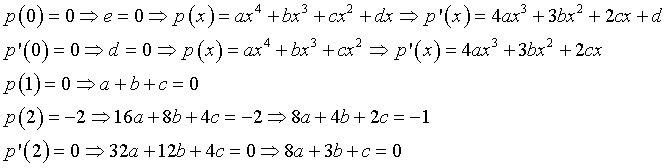
Risolvendo il sistema
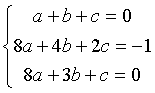
si ottiene
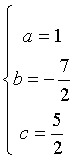
quindi
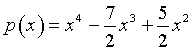
La funzione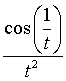 
è la derivata di 
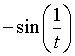dunque
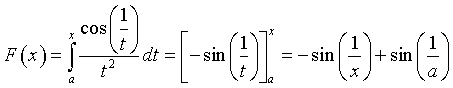
In particolare, indicando con aM il valore massimante di a
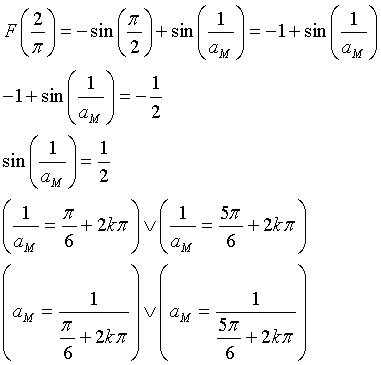
aM è massimante quando il suo denominatore è minimo. Dunque
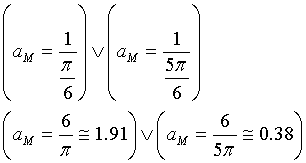
Ovviamente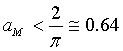 
, quindi
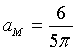
Nel sistema di riferimento cartesiano con asse della ascisse coincidente con la retta PA dal perielio P
all'afelio A,
origine O nel centro del segmento PA e asse delle ordinate perpendicolare alla retta PA per O
si ha xP = -1.47·1011, xA = 1.52·1011,
il semiasse maggiore dell'ellisse misura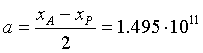 
.
Il fuoco è situato sull'asse delle ascisse con ascissa 
e la misura b del semissa minore è 
.
L'equazione canonica dell'ellisse dell'orbita è quindi
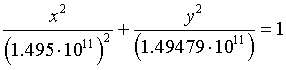
Un esagono regolare di lato l è scomponibile in sei triangoli equilateri equivalenti di lato l con basi sui lati dell'esagono e vertici opposti nel centro dell'esagono.
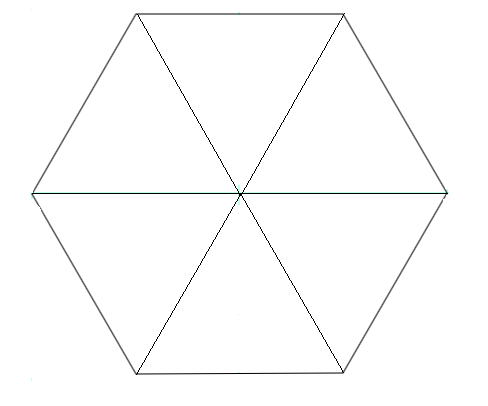
L'altezza h di un triangolo equilatero è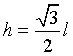 
.
L'altezza di un triangolo equilatero è apotema dell'esagono, dunque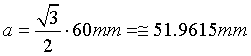 
Poligoni regolari di n lati possono pavimentare un piano solo se ognuno dei loro vertici è comune a k poligoni identici. In generale le misure degli angoli
interni di un poligono di n lati sono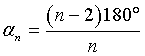
con
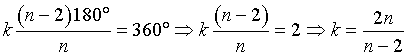. Ovviamente n e k interi con n≥3 e k≥3.
Gli unici valori possibili sono k=3 (triangoli equilateri); k=4 (quadrati); k=6 (esagoni).