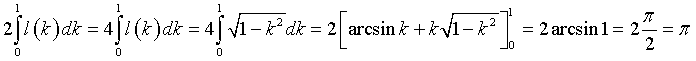![]()
Il discriminante del trinomio ax2+bx+1 è b2-4a e, dato che a<0 è negativo,
la radice quadrata è reale per 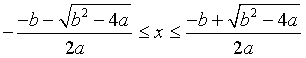 .
Le radici ennesime sono comunque reali quindi questo è il dominio di realtà delle funzioni fn(x).
.
Le radici ennesime sono comunque reali quindi questo è il dominio di realtà delle funzioni fn(x).
fn(0)=-1, quindi il punto P(0,-1) appartiene al grafico di ogni funzione del fascio.
Si ha ![]()
Se x>0 ![]() e
e 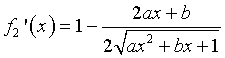
Se x<0 ![]() e
e 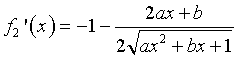
Si ha quindi
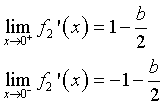
I limiti di f'2(x) per x→0 da destra e da sinistra sono diversi, dunque f2(x) non è derivabile per x=0.
Se n>2 le derivate della radice ennesima sono 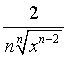 e i loro limiti per x→0
da destra e da sinistra divergono.
e i loro limiti per x→0
da destra e da sinistra divergono.
Quindi il punto angoloso per x=0 si ha per n=2.
Se il grafico di f2(x) è
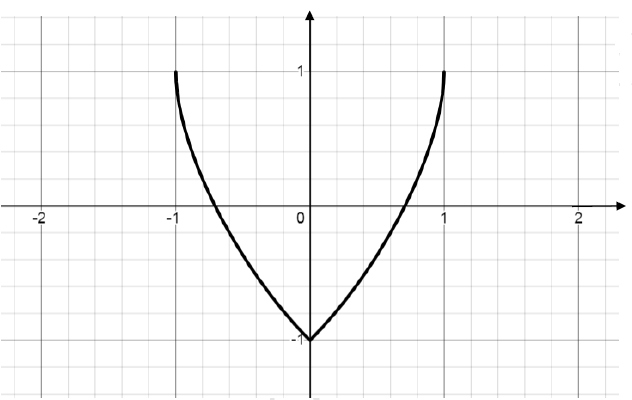
f2(x) è pari, quindi f2(-1) = f2(1)
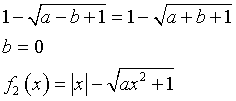
Inoltre f2(1)=1
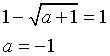
![]()
g(x) è reale per -1≤x≤1.
g(x) è pari. Il suo grafico è simmetrico rispetto all'asse delle ordinate.
g(-1)=1; g(0)=1; g(1)=1
Se x<0, 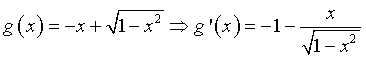
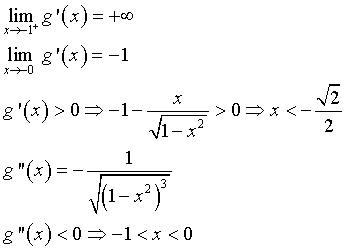
Per x=-1 il grafico ha tangente verticale. La tangente sinistra in x=0 ha coefficiente angolare -1. La funzione è crescente per
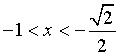 , decrescente per
, decrescente per 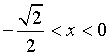 e ha un massimo relativo in
e ha un massimo relativo in 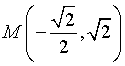 . La funzione ha sempre concavità negativa
. La funzione ha sempre concavità negativa
La parità della funzione implica un andamento simmetrico nell'intervallo ]0;1[.
In particolare si ha un punto angoloso nel punto (0,1).
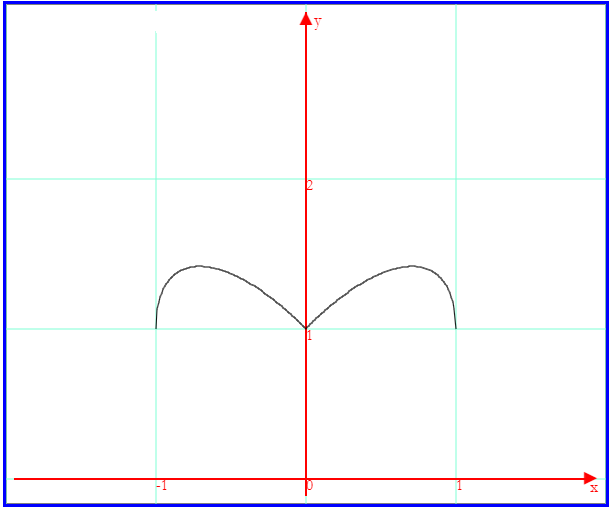
Tracciando insieme le due curve graficate si ha
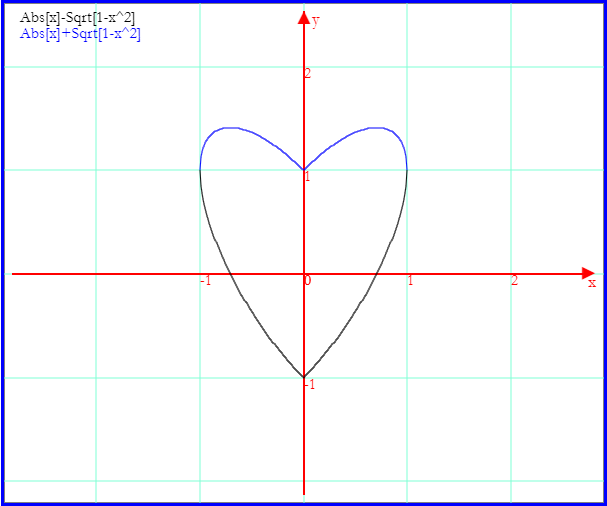
Data la simmetria del grafico, è sufficiente scegliere 0≥k≥1.
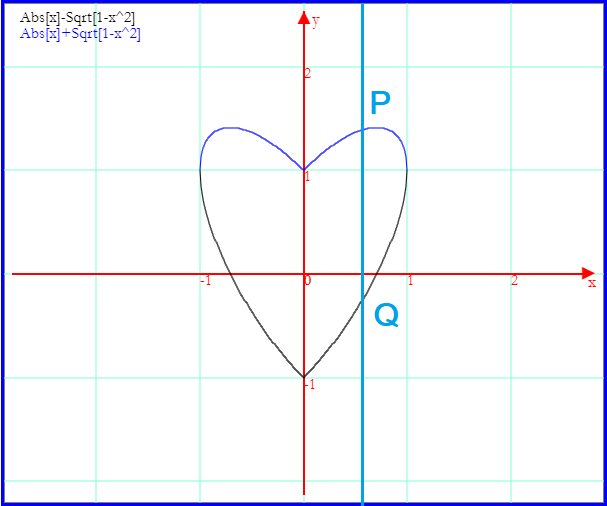
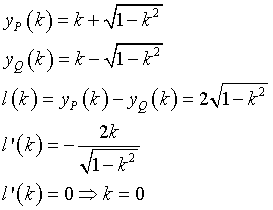
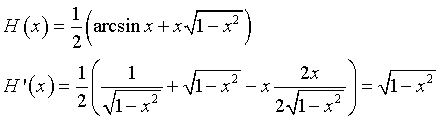
L'area richiesta è data da