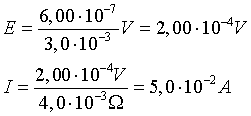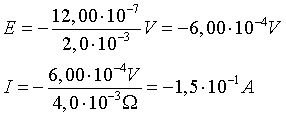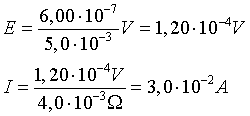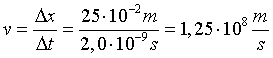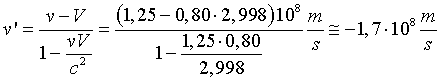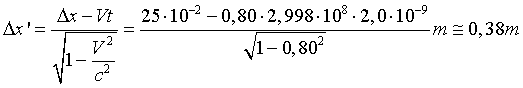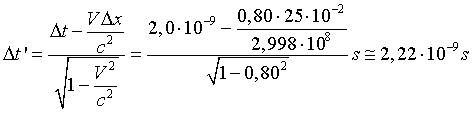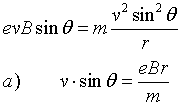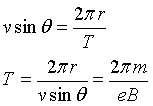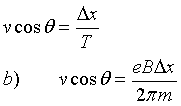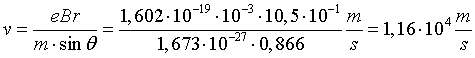Esame di stato 2019 - Liceo Scientifico - Prova di Matematica
Svolgimento del Questionario
Quesito 1
La frazione algebrica 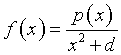 ammette asintoti verticali x = ± 3 se d = -9 e ammette asintoto orizzontale
y = 5 se il numeratore è di secondo grado e il coefficiente del monomio di secondo grado è 5.
ammette asintoti verticali x = ± 3 se d = -9 e ammette asintoto orizzontale
y = 5 se il numeratore è di secondo grado e il coefficiente del monomio di secondo grado è 5.
Inoltre numeratore si annulla per x=0 se ha termine noto nullo e per x=12/5 se è divisibile per x-12/5. Quindi
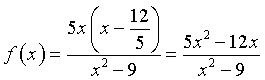
Un estremo relativo deve annullare la derivata prima.
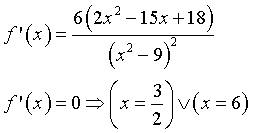
La derivata seconda è
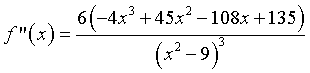 .
.
Si ha f "(3/2) = -32/27, f "(6) = 2/27. Quindi per x=3/2 si ha un massimo relativo, per x=6 si ha un minimo relativo.
In definitiva P(3/2,1) è un massimo, Q(6,4) un minimo.
Quesito 2
Si ha
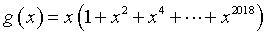
in cui il polinomio tra parentesi ha minimo 1. Quindi il prodotto si annulla solo per x0 = 0.
Il limite richiesto è 0 perché applicando ripetutamente la regola di De L'Hôpital le derivate successive del numeratore calano ripetutamente di grado fino ad azzerarsi,
mentre per le derivate del denominatore si ha
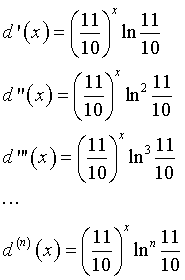
cioè le derivate del denominatore sono sempre prodotti tra numeri positivi e funzioni esponenziali di base maggiore di 1 e tendenti all'infinito.
Quesito 3
Dette rispettivamente x la misura del lato di base e y la misura dell'altezza con x>0 e y>0, si ha
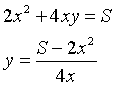
La somma L delle lunghezze degli spigoli è L = 8x+4y.
Quindi
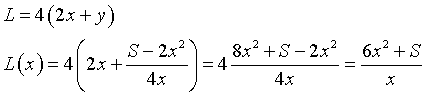
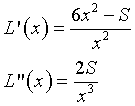
Azzerando L '(x) si ha
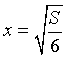
valore per cui la L ''(x) è positiva e quindi minimante.
Si ha inoltre
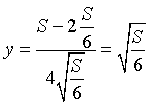
cioè la somma L è minima se il parallelepipedo è un cubo.
Quesito 4
Il luogo geometrico S proposto generalizza nello spazio tridimensionale la circonferenza di Apollonio.
Detta d la misura del segmento AB, si ha
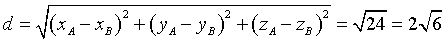
Dette x, y e z le coordinate di un punto P, in un sistema di riferimento con origine in A e asse delle ascisse coincidente con la retta AB, si ha
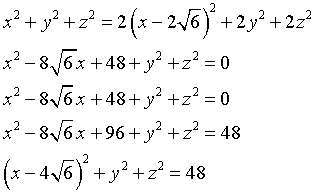
Nel sistema di riferimento adottato si è ottenuta l'equazione di una superficie sferica di raggio r=4√3 e centro (4√6,0,0).
Nel sistema di riferimento originario il centro è il punto della retta AB distante 4√6 da A.
Le equazioni parametriche della retta AB sono
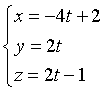
Si ha quindi
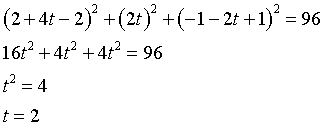
da cui
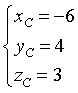
L'equazione di S nel sistema originario è quindi
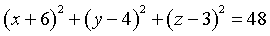
Sostituendo alle variabili nel primo membro le corrispondenti coordinate di T si ottiene 48; dunque T ∈ S
Il vettore TC ha componenti (-4,4,4), dunque l'equazione del piano π tangente è
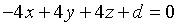
T ∈ π
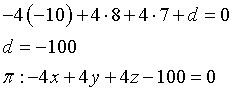
Quesito 5
-
La somma dei quattro numeri è ≤ 5 se esce 4 volte 1 o se esce 3 volte 1 e una volta 2.
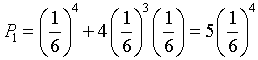
-
Il prodotto è multiplo di 3 se almeno un dado dà 3 o 6. La probabilità che un dado dia un numero diverso è 2/3. La probabilità che esca 4 volte un numero diverso è
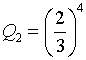
La probabilità che questo non succeda è
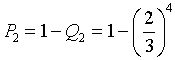
-
La probabilità che un dado dia un numero ≤ 4 è 2/3. La probabilità che questo succeda 4 volte è (2/3)4.
Questa probabilità va diminuita della probabilità che esca 4 volte un numero < 4, cioè (1/2)4.
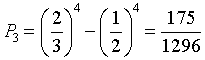
Quesito 6
Per la legge di Faraday la forza elettromotrice (fem) media E in una spira immersa in un campo magnetico variabile di induzione B è
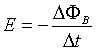 dove ΦB è il flusso di B attraverso una superficie orlata dalla spira. Nel caso più semplice di una spira piana con B uniforme
perpendicolare al piano della spira, ΦB è dato dal prodotto dell'intensità di B per l'area delimitata dalla spira,
con segno positivo se B è diretto verso l'osservatore, altrimenti negativo.
dove ΦB è il flusso di B attraverso una superficie orlata dalla spira. Nel caso più semplice di una spira piana con B uniforme
perpendicolare al piano della spira, ΦB è dato dal prodotto dell'intensità di B per l'area delimitata dalla spira,
con segno positivo se B è diretto verso l'osservatore, altrimenti negativo.
Il segno negativo esprime la legge di Lenz: la corrente provocata dalla fem è tale da produrre a sua volta un campo magnetico che contrasti la variazione di flusso.
Quindi se il flusso cala la corrente circola in senso antiorario e viceversa.
-
Nel primo intervallo
ΔB = -0,20·10-3T
ΔΦB = -0,20·10-3T· 30·10-4m2 = -6,00·10-7T m2
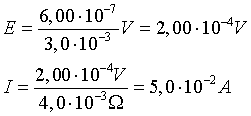
-
Nel secondo intervallo
ΔB = 0,40·10-3T
ΔΦB = 0,40·10-3T· 30·10-4m2 = 12,00·10-7T m2
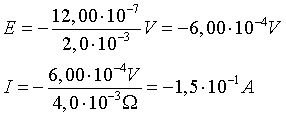
-
Nel terzo intervallo
ΔB = -0,20·10-3T
ΔΦB = -0,20·10-3T· 30·10-4m2 = -6,00·10-7T m2
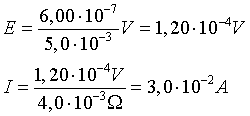
Quesito 7
-
Nel sistema O del laboratorio la particella ha velocità di modulo
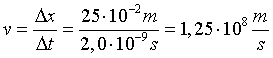
Nel sistema O' della navicella, che ha velocità di trascinamento V, la velocità della particella risulta
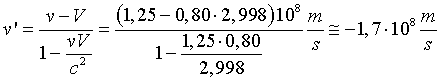
Dalle equazioni di Lorentz, lo spostamento della particella in O' è
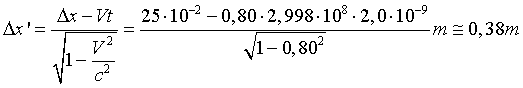
La durata dello spostamento è
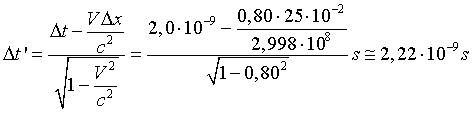
Quesito 8
Detto θ l'angolo tra la velocità v del protone e il campo magnetico di induzione B,
protone è soggetto alla forza di Lorentz di modulo F=evB sinθ. La forza di Lorentz è una forza centripeta, dunque
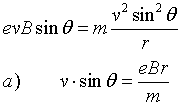
Il periodo di rotazione del protone è tale che
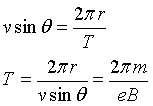
In un periodo l'orbita del protone ha uno spostamento Δx, dunque
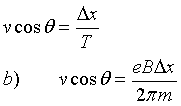
Dividendo membro a membro le identità a) e b) si ottiene

Infine, dalla a) si ottiene il modulo v
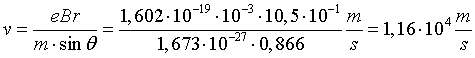
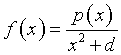 ammette asintoti verticali x = ± 3 se d = -9 e ammette asintoto orizzontale
y = 5 se il numeratore è di secondo grado e il coefficiente del monomio di secondo grado è 5.
ammette asintoti verticali x = ± 3 se d = -9 e ammette asintoto orizzontale
y = 5 se il numeratore è di secondo grado e il coefficiente del monomio di secondo grado è 5.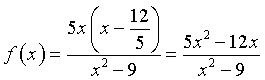
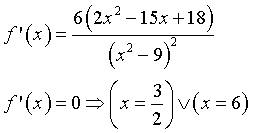
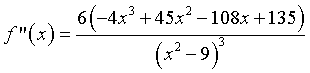 .
.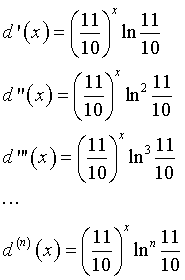
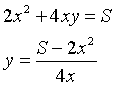
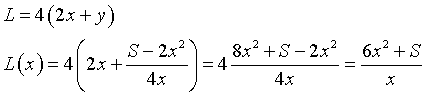
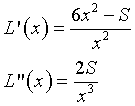
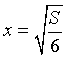
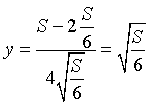
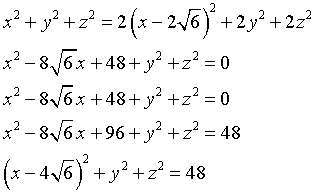
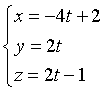
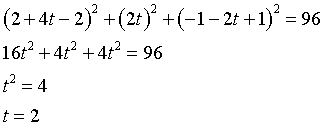
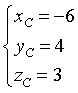
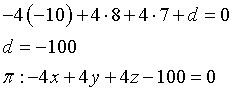
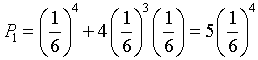
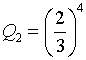
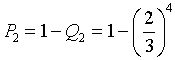
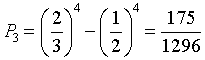
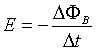 dove ΦB è il flusso di B attraverso una superficie orlata dalla spira. Nel caso più semplice di una spira piana con B uniforme
perpendicolare al piano della spira, ΦB è dato dal prodotto dell'intensità di B per l'area delimitata dalla spira,
con segno positivo se B è diretto verso l'osservatore, altrimenti negativo.
dove ΦB è il flusso di B attraverso una superficie orlata dalla spira. Nel caso più semplice di una spira piana con B uniforme
perpendicolare al piano della spira, ΦB è dato dal prodotto dell'intensità di B per l'area delimitata dalla spira,
con segno positivo se B è diretto verso l'osservatore, altrimenti negativo.