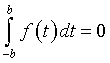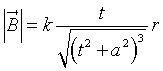
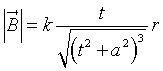
La somma nel radicando è sensata solo se a è un tempo. La frazione è dimensionalmente [T2]. L'induzione B è dimensionalmente [M][T-2][I-1]. r è dimensionalmente [L].
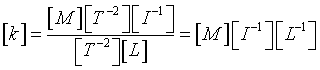
L'unità di misura di k può essere espressa come kg/(A·m).
Nel vuoto, in assenza di correnti e in presenza di un campo elettrico variabile nel tempo, si ha
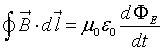
Se ΦE non è costante, B non è nullo.
All'nterno del condensatore le linee di forza di E sono perpendicolari alle armature e dirette dal potenziale alto al potenziale basso. Le linee di forza di B sono circonferenze concentriche centrate sull'asse di simmetria del condensatore. In ogni punto i due campi sono rispettivamente perpendicolari.
La circuitazione di B è
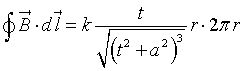
dunque
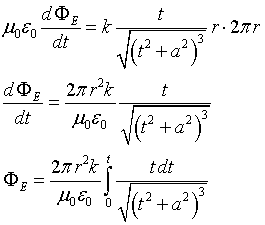
Il calcolo dell'integrale a secondo membro è facilitato dal cambiamento di variabile τ = t2+a2:
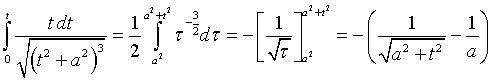
In definitiva
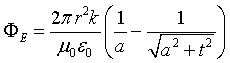
Dividendo il flusso per la superficie si ottiene il campo
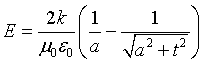
Moltiplicando il campo E per la distanza tra le armature si ottiene la differenza di potenziale V tra di esse.
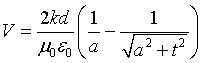
Per t→∞
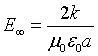
cioè il campo tende ad una costante, la sua derivata tende ad annullarsi e conseguentemente anche B tende ad annullarsi.
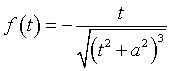
Dal calcolo già svolto nel quesito precedente
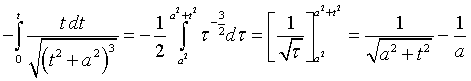
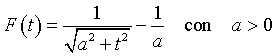
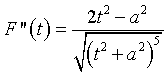
F''(x) ha zeri in ± a/√2; la funzione è convessa per valori esterni all'intervallo delimitato dagli zeri, concava per valori interni e ha flessi obliqui negli zeri.
In particolare
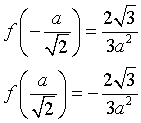
sono i coefficienti angolari delle tangenti nei flessi.
Grafici per a=1
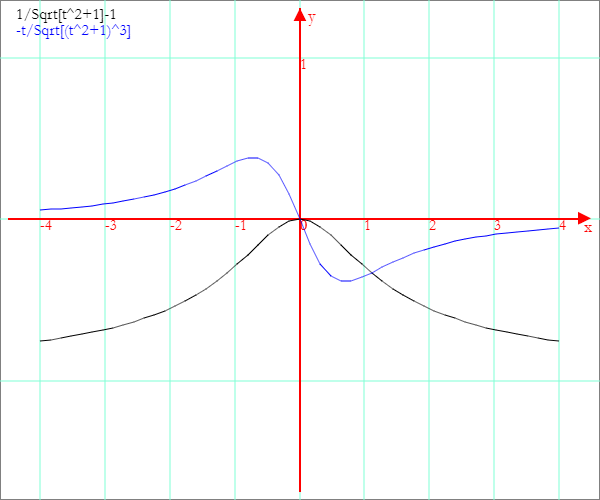
F(t) è continua e derivabile infinite volte, così f(t);
F(t) è pari, quindi f(t) è dispari con grafico simmetrico rispetto all'origine;
dove F(t) ha un estremo, f(t) si annulla;
dove F(t) ha flessi, f(t) ha estremi.
Data la simmetria della curva, l'area richiesta è il doppio dell'integrale di f(t) da -a/√2 a 0.
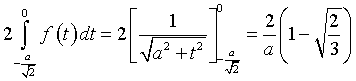
Data la simmetria centrale della curva