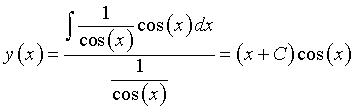Sia y(x) una funzione reale continua incognita della variabile reale x e siano a(x) e b(x) funzioni reali continue note di x. Un'equazione differenziale lineare del primo ordine stabilisce una relazione tra y e la sua derivata prima riducibile alla forma
![]()
Casi paricolari.
Se a(x) = 0, la soluzione è, per definizione,
![]()
Se a(x) costante = a e b(x) costante = 0, l'equazione, detta a variabili separabili, può essere riscritta come
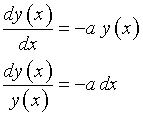
e quindi integrando i differenziali di entrambi i membri
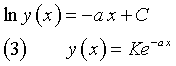
dove C e K sono costanti.
Nel caso generale per la soluzione di questa equazione si può procedere nel seguente modo.
Si definisce la funzione m(x) tale che:
![]()
Indicando con A(x) l'antiderivata di a(x):
![]()
la funzione m(x) può essere espressa come
![]()
Moltiplicando entrambi i membri della (1) per m(x) si ha
![]()
e, per la proprietà (4) di m(x)
![]()
Il primo membro della (6) è la derivata del prodotto m(x)y(x):
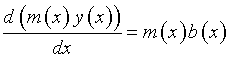
![]()
Integrando entrambi i membri
![]()
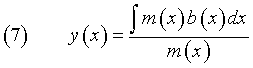
Utilizzando nella (7) l'espressione (5) di m(x) si ottiene
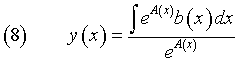
Casi particolari.
a(x) è costante non nulla: a(x) = a
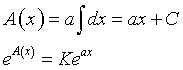
dove C e K sono costanti. Dalla (6) si ha
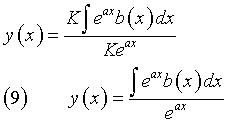
a(x) costante = a e b(x) costante = b
Dalla (9)
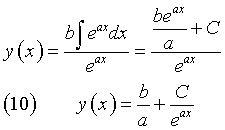
Esempi
![]()
Dalla (3)
![]()
![]()
Dalla (10)
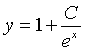
![]()
Dalla (9) si ha
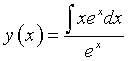
Il numeratore si integra agevolmente per parti e si ottiene
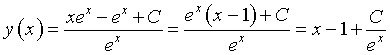
![]()
In questo caso a(x)=tan(x) e b(x)=cos(x) dunque
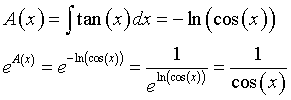
Dalla (6) si ha