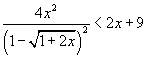
| Esercizi |
| (dalle olimpiadi di matematica) |
1960 - Calcolare l'insieme dei reali che soddisfano alla disequazione
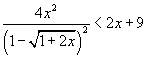
Perché nel primo membro il radicale sia reale e il denominatore non si annulli, deve essere
![]()
In questo dominio il secondo membro è sempre positivo; moltiplicando numeratore e denominatore del primo membro per
![]() si ottiene l'equazione equivalente
si ottiene l'equazione equivalente
![]()
Si ha quindi
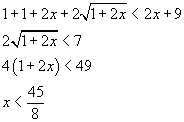
Riunendo le condizioni ottenute si ha
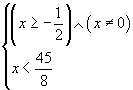
L'insieme soluzione è quindi
![]()
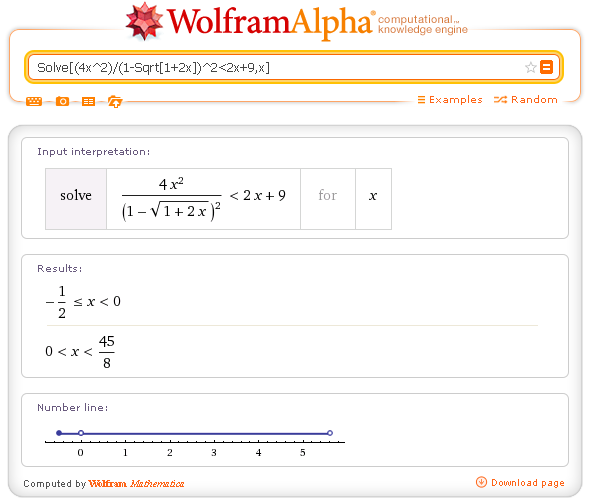
Soluzione della disequazione con WolframAlpha