Un polinomio di primo grado, cioè un binomio di forma
![]()
è una funzione crescente se se a è positivo, decrescente se a è negativo.
Dunque, individuato l'unico zero del binomio
![]()
il binomio è positivo a destra dello zero se è crescente (a>0), è positivo a sinistra dello zero se è decrescente (a<0).
In simboli
![]()
![]()
Esempi.
![]()
![]()
Un polinomio di secondo grado, cioè un trinomio di forma
![]()
può essere espresso nel seguente modo
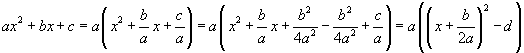
con
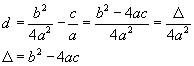
Δ è detto discriminante del trinomio.
Se Δ è negativo, l'espressione tra parentesi, somma di un quadrato con un numero positivo è positiva. Dunque in questo caso il segno del trinomio è costante e coincide con quello di a.
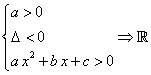
Se Δ è nullo si ha
![]()
Il trinomio è nullo per
![]()
Per ogni altro valore di x il polinomio ha il segno di a.
Quindi
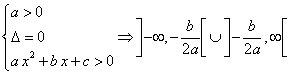
Se Δ è positivo si ha
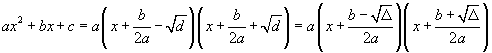
Ponendo
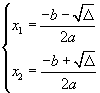
si ha infine
![]()
x1 e x2 sono gli zeri del trinomio (x1 < x2).
Se a è positivo, il trinomio è positivo se i fattori binomi sono concordi in segno
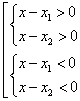
Poiché x2 è maggiore di x1, per assorbimento si ottiene
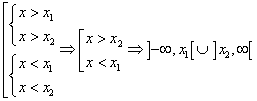
Il trinomio è positivo per valori esterni all'intervallo degli zeri.
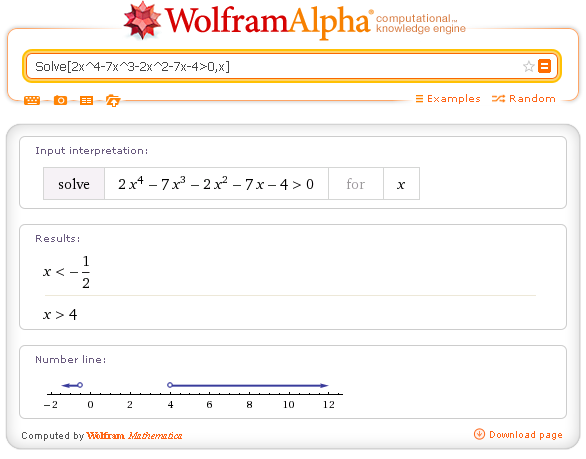
Un esempio con WolframAlpha:
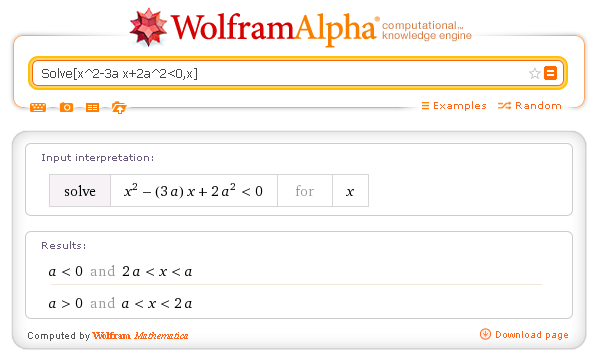
Per polinomi di grado superiore al secondo lo studio del segno è praticabile agevolmente quando si riesce a scomporre il polinomio in prodotto di potenze di fattori di primo o secondo grado.
Ricordando il principio già applicato per i trinomi di secondo grado, cioè che dall'analisi del segno di ogni singolo fattore è possibile dedurre il segno del loro prodotto, cioè del polinomio.
Operativamente è sufficiente analizzare solo il segno dei fattori di segno variabile, trascurando, perché ininfluenti, i fattori di segno costantemente positivo.
Esempio:
![]()
Poiché P(4)=0, il polinomio è divisibile per x-4.
Si ottiene
![]()
Il fattore di terzo grado è scomponibile con raccoglimento a gruppi. Si ottiene
![]()
Il fattore di secondo grado è costantemente positivo, dunque non influisce sul segno del prodotto. È quindi sufficiente studiare il segno del prodotto dei fattori di primo grado. Tale prodotto equivale ad un trinomio di primo coefficiente positivo (2) e di zeri
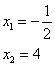
Dunque il polinomio studiato è positivo in
![]()
La stessa disequazione con WolframAlpha: