In molte situazioni teoriche e applicative risulta importante stabilire per quali valori del suo argomento reale x una funzione
reale si azzera.
Le modalità di risoluzione di questo problema sono studiate dalla teoria delle equazioni, con metodi diversi a seconda del
tipo di funzione (algebrica, esponenziale, trigonometrica, ecc.).
L'insieme dei valori che annullano una funzione (detti zeri della funzione) è solitamente un insieme discreto, cioè
contenente un numero finito o infinito di numeri reali 'isolati' l'uno dall'altro.
Ad esempio, per la funzione
![]()
l'insieme degli zeri è
![]()
mentre per la funzione
![]()
l'insieme degli zeri è
![]()
Soluzione dell'equazione con WolframAlpha
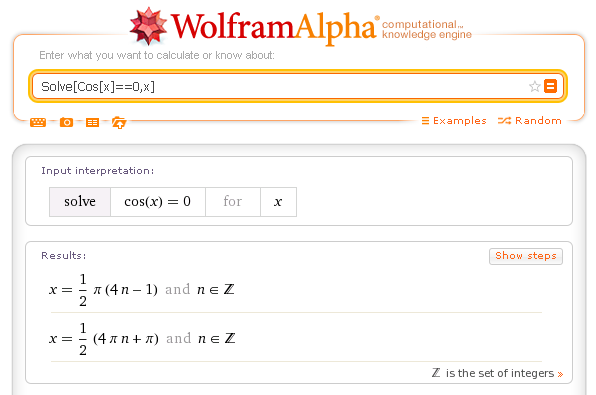
Il problema dell'individuazione degli zeri di una funzione si generalizza nello studio del segno della funzione stessa, cioè
nell'individuazione, oltre che dell'insieme degli zeri, dell'insieme in cui la funzione è positiva (dominio di positività)
e dell'insieme in cui la funzione è negativa.
Questi insiemi sono solitamente intervalli o unioni di intervalli.
Va sempre tenuto ben presente che tali insiemi devono essere sottinsiemi del dominio di realtà delle funzione, che a sua volta è sottinsieme del dominio di esistenza della funzione.
Ad esempio, la funzione
![]()
ha come dominio di esistenza R-{-1,1} perché le frazioni nei radicandi non sono definite per -1 e 1;
ha come dominio di realtà ]-∞,-1[U]1,∞[ perché la funzione è reale solo se i radicandi non sono negativi ma, in questo caso, per la condizione di esistenza, nemmeno nulli.
Quindi per sviluppare un studio di segno di funzione, in generale, vanno innanzitutto individuati i domini di esistenza e di realtà.
Conviene poi determinare il dominio di positività imponendo la condizione di positività della funzione
![]()
Nell'esempio proposto queste operazioni implicano l'impostazione del sistema di condizioni
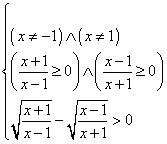
L'intersezione tra i tre insiemi individuati dalle tre condizioni, che può essere effettuata servendosi di rappresentazioni grafiche degli stessi, permette di definire l'insieme P (dominio di positività).
![]()
La definizione dell'insieme P implica anche la definizione del dominio di non positività della funzione, cioè del complementare di P
![]()
Questo insieme non coincide con il dominio di negatività
![]()
N però può essere facilmente ottenuto eliminando gli zeri dal complementare di P.
Risolvere una disequazione significa stabilire l'insieme in cui una funzione f(x) supera un'altra funzione g(x)
![]()
Questo problema è del tutto equivalente a
![]()
e si riconduce quindi allo studio del segno della funzione
![]()
Ci si limiterà in questa sede allo studio del segno delle funzioni algebriche: polinomi, frazioni, radicali e moduli.
In generale