Quesito 1

Si è osservato che un corpo di massa M=40 g , lasciato cadere in un liquido, dopo una fase transitoria, si muove con velocità costante V=24,5 cm/s e che lo stesso corpo, collegato ad una molla, inizialmente fermo e spostato di 10 cm dalla sua posizione di equilibrio (molla indeformata), nel vuoto oscilla con una pulsazione Ω=50 s^-1.

Calcolare, date le stesse condizioni iniziali ma con il sistema completamente immerso nel liquido:

1. il periodo di oscillazione del sistema molla-corpo (pseudoperiodo);
2. dopo quanto tempo l'ampiezza delle oscillazioni si riduce ad un decimo di quella iniziale;
3. quale dovrebbe essere il coefficiente di smorzamento per avere lo smorzamento critico;
4. in caso di smorzamento critico, in quanto l'ampiezza delle oscillazioni diventerebbe un decimo di quella iniziale.

Quesito 2

Si è osservato che un oscillatore armonico, di massa M=1Kg e costante elastica k = 100 N/m, oscillando in un mezzo viscoso, dimezza l'ampiezza delle proprie oscillazioni ogni 5 secondi. Calcolare:

1. il coefficiente di smorzamento;
2. la pulsazione di una forza eccitatrice esterna capace di produrre le condizioni di risonanza;
3. il modulo del massimo spostamento dalla posizione di equilibrio in condizioni di risonanza se il massimo valore della forza eccitatrice è di 5 N.

Svolgimento del quesito 1

Per determinare il valore assoluto del coefficiente di smorzamento β si uguaglia l'intensità del peso all'intensità dell'attrito viscoso che, in prima approssimazione, è direttamente proporzionale alla velocità:

La costante elastica della molla risulta

Il discriminante dell'equazione caratteristica è (in unità S.I.)

quindi il moto è sottocritico con pulsazione

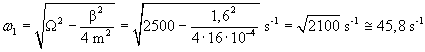
1. Lo pseudoperiodo T₁ risulta quindi

   

2. L'equazione oraria del moto risulta

   

   L'ampiezza dell'oscillazione è

   

   L'ampiezza iniziale è A(0)=C₁. Il tempo richiesto si ottiene risolvendo l'equazione

   

3.  

   

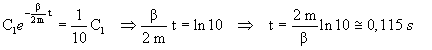
4. In caso di smorzamento critico l'equazione oraria del moto è

   

   Sostituendo i valori di m e β si ha quindi

   

   La velocità istantanea è

   

   Il corpo è inizialmente fermo:

   

   e l'equazione oraria può essere scritta

   

   da cui

   

   L'equazione da risolvere è quindi

   

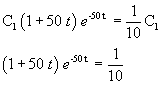
   Per facilitare un'approssimazione della soluzione si può porre τ = 50 t

   

   Arrotondando al centesimo i valori della funzione

   

   si ha

   τ	f(τ)
   0	1,00
   1	0,73
   2	0,41
   3	0,20
   4	0,09

   La soluzione è molto prossima a 4, quindi

   

Svolgimento del quesito 2

1. L'equazione oraria del moto è

   

   in cui l'ampiezza è

   

   Si ha quindi

   

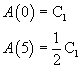
   L'equazione da risolvere è

   

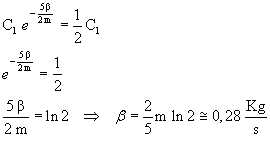
2. La pulsazione Ω deve coincidere con la pulsazione propria dell'oscillatore

   

3. In condizione di risonanza il valore massimo dell'ampiezza di oscillazione risulta