Quesito 1

Un corpo puntiforme P, di massa M_P=2 Kg, si muove per azione della sola forza

Sapendo che nell'istante t₀ = 0 s P è fermo nell'origine, determinare:

1. il momento di F rispetto all'origine nell'istante t₁ = 2 s;
2. le componenti normale e tangenziale dell'accelerazione di P nell'istante t₁;
3. il lavoro compiuto da F nei primi 2 secondi.

All'istante t₁ la forza F cessa di agire e il corpo esplode in due frammenti A e B tali che la massa M_A di A è tripla della massa M_B di B. Sapendo che la velocità di A è

4. calcolare la velocità di B.

Risoluzione

1)

Dall'espressione della forza in funzione del tempo si ricava, dividendo per la massa, l'accelerazione e quindi, con successive integrazioni, la velocità e la posizione:

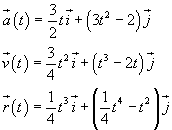
Per t=2 s si ha

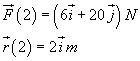
e quindi il momento τ della forza è

2)

Per t=2 s si ha

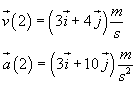
Il versore tangenziale è

e quindi la componente tangenziale dell'accelerazione è

Sottraendo dal quadrato dell'accelerazione il quadrato dell'accelerazione tangenziale si ottiene il quadrato dell'accelerazione normale di cui si estrae la radice:

3)

Dal quadrato di v(2) si ottiene l'energia cinetica il cui valore coincide con il lavoro della forza:

4)

Moltiplicando v(2) per la massa si ha la quantità di moto Q_S del sistema prima dell'esplosione che equivale alla somma delle quantità di moto Q_A e Q_B dei frammenti di masse rispettivamente di 1,5 Kg e 0,5 Kg.

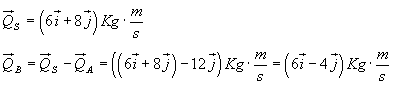
Infine, dividendo Q_B per la massa di B si ottiene la velocità di B: