Quesito 1

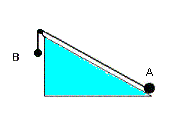
Un corpo A di 2 kg di massa è appoggiato su un piano inclinato di 30° rispetto al terreno orizzontale ed è collegato da una fune inestensibile di massa nulla che scorre senza attriti su una carrucola ad un corpo B di 5 kg di massa che può cadere verticalmente.

Supponendo dapprima che tra A e il piano l'attrito sia trascurabile:

1. Calcolare il modulo dell'accelerazione del sistema in movimento.
2. Calcolare la tensione cui è sottoposta la fune.

Rispondere poi ai quesiti a) e b) nel caso in cui il coefficiente di attrito dinamico tra A e il piano sia μ=0,4.

Risoluzione

a)

Sul corpo B agiscono la tensione T_B diretta verso l'alto e la forza peso F_B diretta verso il basso con intensità

Sul corpo A agiscono la tensione T_A diretta verso sinistra, di modulo uguale a quello di T_B, e la forza peso. La componente normale della forza peso è equilibrata dalla reazione del vincolo perpendicolare al piano, quindi è efficace solo la componente del peso parallela al piano la cui intensità è

Data la flessibilità della fune il problema è sostanzialmente unidimensionale e può essere impostato scalarmente assegnando, ad esempio, segno positivo per la parte scalare dei vettori diretti verso sinistra e segno negativo per quella dei vettori diretti verso destra.

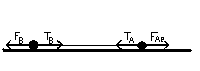
La somma delle tensioni è nulla. La risultante delle forze sul sistema è F_B-F_Aeff che per il secondo principio della dinamica è uguale alla massa totale M_A+M_B per l'accelerazione a

Risulta quindi

Il segno positivo dell'accelerazione indica che il sistema slitta in senso antiorario: B cala, A sale.

b)

Considerando, ad esempio, il corpo B, si osserva che esso si muove con l'accelerazione trovata, sotto l'azione delle forze tensione e peso: per il secondo principio della dinamica si può scrivere

a')

La forza di attrito R agente sul corpo A è proporzionale alla componente normale del peso di A e risulta, in modulo,

La risultante di tutte le forze agenti sul sistema, con le convenzioni adottate, risulta

da cui si deduce

b')

Procedendo come nel caso b) si ottiene, con il nuovo valore di a,

Quesito 2

L'estremo libero di una molla vibra con un periodo di 2 secondi quando ad esso viene fissata una massa m. Quando tale massa viene aumentata di 2 Kg il periodo diventa di 3 secondi.

Calcolare il valore di m e della costante elastica k.

Risoluzione

Ricordando che il periodo T di oscillazione di una molla ideale (con tutta la massa concentrata in un estremo) è

dai valori proposti si ottiene

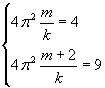
Dividendo le due equazioni membro a membro si ottiene

Infine dalla prima delle due equazioni si ha