Un proiettile, lanciato orizzontalmente con velocità di modulo v0 da un'altezza h=120 m impatta sul suolo pianeggiante in un punto P con una velocità di modulo vf = 7v0.
a)
La coordinata y in funzione del tempo è espressa da
![]()
Per y finale=0 si ottiene
![]()
La velocità finale è quindi
![]()
e dato che il suo modulo è settuplo del modulo iniziale, si ha
![]()
In definitiva
![]()
b)
La velocità finale risulta
![]()
c)
Il versore della velocità finale è
![]()
L'accelerazione è costante e vale
![]()
La sua componente tangenziale è
![]()
e quindi la componente normale dell'accelerazione
![]()
In definitiva
![]()
La posizione di un punto P, che ruota sul piano xy in senso antiorario attorno all'origine O
con velocità di modulo costante
![]() , al tempo
t0=0 s è
, al tempo
t0=0 s è
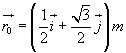
In un moto circolare il raggio R è costante e coincide con il modulo della posizione in un istante qualunque. Quindi R =1 m.
La fase φ0 della posizione iniziale deve essere tale che
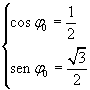
Risulta quindi
![]()
Se il modulo della velocità è costante, anche il modulo della velocità angolare è costante.
![]()
L'equazione oraria del moto circolare è quindi
![]()
da cui seguono
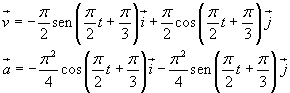
Per t1=2 s si ha
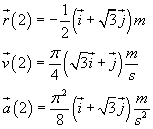
b)
Da
![]()
per ω0=π/2, ω=0 e t=1s si ha
![]()
c)
Da
![]()
per
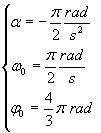
si ottiene
![]()
![]()