Se una particella di massa m è attratta dall'origine O con una forza inversamente proporzionale al quadrato della sua distanza x (x > 0), la sua energia potenziale è espressa da una funzione di forma
![]()
dove C è una costante di proporzionalità positiva che dipende dalla particella, dalla sorgente e dal mezzo. In questo caso la buca di potenziale ha forma
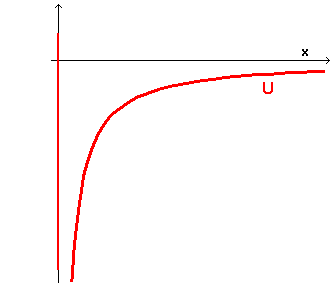
Se si assume negativa l'energia totale della particella, il diagramma dell'energia è il seguente
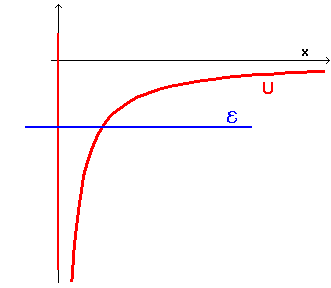
L'equazione di Schroedinger in questo caso è
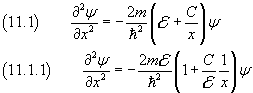
Introducendo la variabile ξ
![]()
si ha
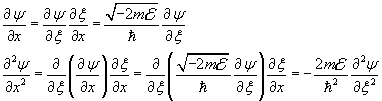
e dalla (11.1.1) si ha
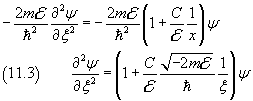
Per alleggerire la notazione si pone
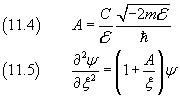
Per x→∞, la ψ si deve annullare. Si può quindi congetturare che
![]()
dove φ è una funzione da determinare sapendo che ha una singolarità per ξ=0 e che deve essere finita per ogni ξ.
Derivando due volte la (11.6) rispetto a ξ si ha
![]()
Sostituendo questa derivata nella (11.5) si ottiene
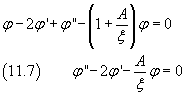
Come nel paragrafo precedente si assume che φ sia sviluppabile in serie di potenze
![]()
e quindi
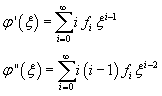
Sostituendo nella (11.7)
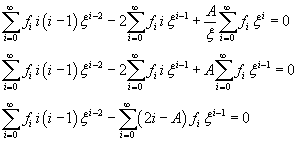
Poiché φ non è definita per x=0, nello sviluppo non si considerano le potenze negative di ξ
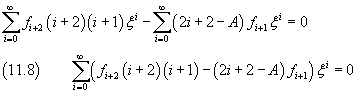
La sommatoria in (11.8) si annulla se sono nulli tutti i coefficienti delle potenze di ξ
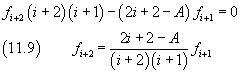
Si è così ottenuta una relazione ricorsiva che connette ogni coefficiente dello sviluppo di φ al precedente. Perché lo sviluppo si riduca a un polinomio, in modo che φ abbia comunque un valore finito, è necessario che da un certo indice k in poi, tutti i coefficienti siano nulli. In particolare
![]()
cioè, A deve essere un numero pari non nullo (nella (11.10) n rappresenta un numero naturale ≥ 1).
Riprendendo dalla (11.4) la definizione di A e utilizzandola nella (11.10) si ha
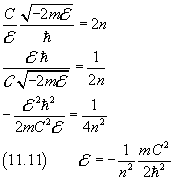
Anche in questo caso, come in quelli esaminati nei paragrafi precedenti, si conclude che l'energia di una particella può assumere solo valori discreti. Il minimo valore possibile è
![]()
Nel caso che la particella sia un elettrone nel campo elettrico di un protone, si ha
![]()
e dalla (11.1) si ha
![]()
La (11.13) coincide con l'espressione dell'energia di un elettrone in orbita circolare attorno a un protone calcolata da Bohr per spiegare lo spettro dell'idrogeno, imponendo che il modulo del momento angolare l dell'elettrone debba essere un multiplo intero della costante di Planck ridotta
![]()
Infatti, indicando con r il raggio dell'orbita e con v la velocità dell'elettrone
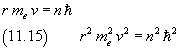
Uguagliando forza di Coulomb e forza centripeta
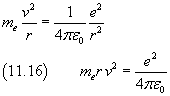
Dividendo membro a membro la (11.16) per la (11.15)
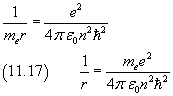
L'energia totale classica di un elettrone in orbita circolare attorno a un protone è
![]()
Infine, sostituendo l'espressione di r della (11.17) nella (11.18) si ha ottiene la (11.13)
Quindi l'equazione di Schroedinger offre un fondamento generale a risultati ottenuti precedentemente sulla base di ipotesi 'ad hoc', come quelle di Bohr, assunte per giustificare specifici risultati sperimentali.