Quando si osserva che un corpuscolo C, situato nella posizione r rispetto ad un opportuno sistema di riferimento, è sottoposto ad una forza f che dipende dalla posizione r, si assume che la forza f sia dovuta alla presenza, nello spazio in cui si muove C, di una grandezza fisica di natura vettoriale h(r), funzione delle coordinate di posizione e del tempo, detta campo e che il valore di f risulti dal prodotto tra il valore di una proprietà scalare costante q del corpuscolo (la sua carica) per h:
![]()
Quindi anche il campo h è una grandezza vettoriale funzione della posizione r.
Nelle considerazioni successive si assume che h sia una funzione continua e derivabile almeno due volte rispetto alla coordinate cartesiane (x,y,z) della posizione r.
Il lavoro di una forza f che produce uno spostamento infinitesimo dr è definito dal differenziale
![]()
Quando questo differenziale è un differenziale esatto, cioè quando esiste una funzione scalare φ(x,y,z) tale che
![]()
allora il lavoro compiuto da f per spostare il suo punto di applicazione dalla posizione rA alla posizione rB è dato da
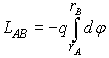
e, per il teorema fondamentale del calcolo integrale, dipende solo dagli estremi del percorso e non dalla particolare traiettoria compiuta da C:
![]()
In questo caso la forza f si dice conservativa e la funzione scalare φ è detta potenziale scalare. Questa definizione di φ implica che il potenziale scalare è definito a meno di una costante additiva.
È immediato dedurre che il lavoro di una forza conservativa lungo un percorso chiuso è nullo:
![]()
Un campo h che genera un forza conservativa è, a sua volta, detto campo conservativo. Per h si avrà:
![]()
L'integrale circolare
![]() è detto circuitazione di h.
è detto circuitazione di h.
La circuitazione di un campo conservativo è nulla.
Viceversa
se la circuitazione di un campo è nulla, il campo è conservativo.