Arcobaleno

L'arcobaleno è certamente uno degli spettacoli più suggestivi offerto dalla natura ed è stato ammirato con stupore dagli uomini fin dalla più remota antichità. Nella Bibbia è stato interpretato come segno di pace eterna tra Dio e tutte le creature.

"Questo sarà il segno del patto che io faccio tra me e voi e tutti gli esseri viventi che sono con voi, per tutte le generazioni in perpetuo: io pongo il mio arco tra le nubi e servirà di segno del patto tra me e la terra. Quando accumulerò delle nubi sopra la terra e si vedrà l'arcobaleno nelle nubi, allora io mi ricorderò del patto tra me e voi e tutti gli esseri viventi di ogni specie e le acque non diventeranno più un diluvio per distruggere ogni carne. L'arcobaleno sarà nelle nubi e io, guardandolo, mi ricorderò del patto perpetuo fra Dio e ogni essere vivente, di qualunque specie, che è sulla terra. (Genesi 9, 12-16)."

In ambiente greco l'indagine rigorosa e razionale sulle caratteristiche dell'arcobaleno e sulle loro cause, come sezione particolare di una più generale ricerca sulla natura della luce e dei fenomeni luminosi, fu intrapresa da quasi tutti i filosofi, ad esempio da Epicuro, la cui dottrina fu esposta in forma poetica da Lucrezio:

Hic ubi sol radiis tempestatem inter opacam
adversa fulsit nimborum aspargine contra
tum color in nigris existit nubibus arqui.
(De rerum natura: VI, 524-526)
Quando il sole nella buia tempesta risplende con i suoi raggi di fronte all'opposta accozzaglia di nembi, allora si forma tra le nere nubi l'arcobaleno.

Una descrizione molto più asettica, ma molto più attenta e dettagliata, è data da Aristotele nel libro III della sua Meteorologia:

L'arcobaleno non forma mai un'intera circonferenza e nemmeno un arco maggiore di una semicirconferenza. Al tramonto e all'alba lo spessore dell'arco è stretto e l'arco ha la massima estensione. Quando il sole si alza maggiormente nel cielo lo spessore si allarga e la lunghezza dell'arco si riduce. Dopo l'equinozio d'autunno, nei giorni più corti, può essere visto a qualunque ora del giorno; in estate non non può essere visto nelle ore del mezzogiorno. Non ci sono mai più di due arcobaleni nello stesso tempo. Ognuno di essi ha tre colori. I colori sono gli stessi in entrambi e il loro numero è identico, ma nell'arcobaleno esterno sono più deboli e la loro posizione è invertita. Nell'arcobaleno interno la prima e più larga striscia è rossa; in quello esterno la striscia più vicina a quello interno è dello stesso colore ma più stretta. Per le alte strisce vale lo stesso principio. Queste hanno gli unici colori che i pittori non possono fabbricarsi, dato che ci sono colori da essi creati con misture, ma nessuna mistura può dare il rosso, il verde e il blu. Questi sono i colori dell'arcobaleno, per quanto talora tra il rosso e il verde si possa vedere il giallo.

Aristotele non fa menzione del fatto che tra i due archi c'è una zona buia, menzionata per la prima volta da Alessandro di Afrodisia (circa 200 d.C.) oggi denominata 'banda scura di Alessandro'.

Aristotele non nota che, se il sole è abbastanza alto rispetto all'orizzonte, può succedere di vedere un tratto di arcobaleno invertito.

Aristotele offre, nel seguito del libro, una spiegazione dettagliata di tutte le cose osservate, che, oggi, risulta inadeguata fondamentalmente per due motivi:

Può essere interessante osservare che l'opinione aristotelica sul numero dei colori dell'arcobaleno (tre o quattro) fu tranquillamente accettata fino a che Newton (1643-1727), con i suoi studi sulla scomposizione della luce solare con un prisma, ne classificò sette.

L'argomento, nell'antichità, fu poi ripreso da numerosi autori: vanno ricordate le opere specialistiche sull'ottica di Euclide e di Tolomeo.

Mentre nel medio evo in Europa la maggior parte degli studiosi continuò ad accettare passivamente le opinioni degli antichi, discutendo se il numero dei colori era di tre (come le persone della Trinità) o di quattro (come i quattro elementi empedoclei) un grande scienziato arabo, Ibn Al Haytham (965-1038), noto in Europa con il nome di Alhazen, migliorò di molto la comprensione dell'argomento scoprendo il fenomeno della rifrazione, anche se non riuscì a ricavarne la legge.

Contemporaneamente (probabilmente c'era qualche forma di comunicazione tra i dotti dell'epoca) in occidente l'opera di Alhazen, tradotta in latino (De aspectibus o Perspectiva), fu ripresa da Roger Bacon (Opus maius) che nel 1266 misurò l'angolo dell'arcobaleno in 42° (quello secondario è di 8° gradi più alto nel cielo). Nel 1304 il monaco tedesco Teodorico di Freiberg (De iride) propose l'ipotesi che ogni goccia d'acqua delle nubi faccia il suo proprio arcobaleno e verificò la sua ipotesi osservando la rifrazione della luce solare in un fiasco sferico. I risultati di Teodorico rimasero sconosciuti per tre secoli. Furono riproposti alla cultura occidentale solo all'inizio del diciassettesimo secolo, prima da Marco Antonio de Dominis nel 1611, poi da Cartesio (René Descartes) nel 1637 e da Giovan Battista Hodierna (1647).

Cartesio semplificò lo studio dell'arcobaleno riducendolo allo studio di una goccia d'acqua e del modo con cui essa interagisce con la luce che la colpisce e poté avvalersi della formulazione matematica della legge della rifrazione esposta nel 1621 da W. Snell.

Un po' di matematica.

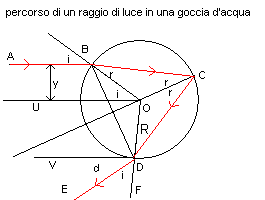
Ragionando sul modello proposto da Cartesio, si consideri un singolo raggio di luce solare AB, per ipotesi monocromatico e orizzontale: come osservava Aristotele, l'arcobaleno si vede quando il sole non è troppo alto nel cielo; in presenza dell'arcobaleno, in prima approssimazione, si possono considerare i raggi solari paralleli al terreno.
Il raggio dista y dalla retta orizzontale UO passante per il centro O della sfera. y è detto parametro di impatto. Indicando con R il raggio della sfera, si ha

Il raggio penetra nella sfera nel punto B formando un angolo di incidenza di misura i con la normale alla superficie, la retta radiale OB, e viene rifratto seguendo il percorso BC che forma un angolo di rifrazione di misura r con la normale OB.

dove n rappresenta l'indice di rifrazione dell'acqua per il particolare colore considerato.
Si ottiene quindi

Il raggio incontra la superficie della sfera in C. Parte della sua energia fuoriesce dalla sfera, ma parte viene riflessa seguendo il percorso CD, che, per la legge della riflessione, forma un angolo di misura r con la normale OC.

Il raggio CD incontra la superficie in D e di nuovo una parte viene riflesso e una parte fuoriesce seguendo il percorso DE e formando un angolo di misura i con la normale OD. La parte che fuoriesce, colpendo l'occhio dell'osservatore, origina l'arcobaleno primario. La parte riflessa colpirà ancora la superficie interna della sfera e ancora in parte ne uscirà venendo rifratta. Questa seconda emissione è quella che dà origine all'arcobaleno secondario. Per non complicare troppo figure e calcoli si analizza qui solo la formazione dell'arcobaleno primario.

Il raggio DE, rispetto all'orizzontale DV forma l'angolo VDE, di misura d che si può ottenere per differenza tra quelle degli angoli FDV e FDE, cioè i.

A sua volta FDV, per il parallelismo, è congruente con FOU.
FOU può, a sua volta, essere ottenuto per differenza tra BOD e BOU.
Ma BOD, doppio di BCD, misura 4r e BOU misura i. In definitiva si ottiene

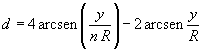
La deflessione non dipende dal raggio R della sfera, ma solo dall'indice di rifrazione n e, dato che questo indice varia al variare della lunghezza d'onda λ, ad ogni colore corrisponde una diversa deflessione; quindi una goccia d'acqua, come un prisma, produce una dispersione dei colori.

Il parametro y varia da 0 a R; graficando d in funzione di y in questo intervallo, per n=1.33 che è l'indice di rifrazione del rosso nell'acqua, si ottiene:

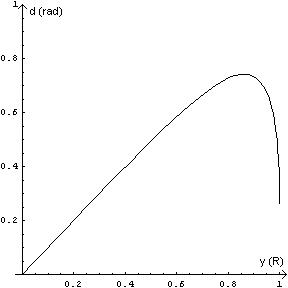
L'angolo di deflessione d cresce al crescere di y e raggiunge un massimo attorno a 9/10 del raggio; questo massimo è di circa 0,75 radianti. Nessuno dei raggi solari subisce una deflessione maggiore: fisicamente questo significa che guardando il cielo sopra l'arcobaleno non si riceve luce e si spiega così la banda scura di Alessandro.

Uguagliando a zero la derivata prima di d si può ottenere più esattamente il valore del parametro y con deflessione massima e quindi il valore di tale deflessione.

Calcolando l'angolo di deflessione massima per alcuni colori si ottengono i seguenti valori:

λ (nm)	colore	n	d_max (rad)	d_max (gradi)
706,5	rosso	1,3300	0,742051	42°30'59"
589,3	giallo	1,3330	0,734402	42°04'41"
501,6	verde	1,3364	0,725817	41°35'10"
404,7	viola	1,3427	0,710143	40°41'18"

Approfondimenti

Con un metodo simile a quello proposto è possibile ricavare dati analoghi per l'arcobaleno secondario e spiegarne le caratteristiche rilevate da Aristotele e da R. Bacon.

I risultati ottenuti con il modello di Cartesio, basato sulle semplici leggi dell'ottica geometrica, spiegano in modo soddisfacente le caratteristiche fisiche principali dell'arcobaleno, ma non rendono conto di altre come, ad esempio, la presenza di archi soprannumerari nella parte più luminosa dell'arco, l'andamento dell'intensità dei colori, i fenomeni di polarizzazione.

La spiegazione di questi aspetti ha impegnato i ricercatori del Settecento (Young), dell'Ottocento (Airy) e impegna ancora i fisici contemporanei che hanno sviluppato sofisticati modelli fisico-matematici basati sulla teoria ondulatoria della luce e sulla meccanica quantistica. Per una rassegna dettagliata di queste ricerche e per l'illustrazione di interessanti esperienze che si possono realizzare a scuola o anche a casa, consultare:

Un po' di storia.

Un po' di matematica.

Approfondimenti