Newtonian mechanics is based on three well-known principles, the first of which, known as the principle of inertia, is commonly stated in textbooks as follows: a free physical point continues in a state of rest, or of uniform motion in a straight line.
This proposition may seem trivial to students (and perhaps even to authors of textbooks) and this feeling can be justified by the fact that, after his ritual enunciation, it practically disappears from the the teaching of Physics.
But the fundamental meaning of this statement is by no means trivial. This is proven by the fact that it was formulated only in the seventeenth century, when Galileo and Newton were able to conceive it clearly, and that another 300 years passed before Einstein could develop all its implications and reach conclusions quite different than those suggested by common sense.
The word 'free point' does denote a point-like body, with finite and constant mass m, not influenced by any outside presence, whose behavior is no different from what it would if it were alone in the whole universe.
It should be noted that this is a big abstraction with respect to the concrete experience of things.
For example, in nature there are no point-like bodies: every body, big or small, has extension. But, worse, the idea itself of point-like body is theoretically absurd: such a body would have infinite density.
In addition, throughout the Universe there are no free points, because all the bodies in the Universe are subject to the gravitational pull of other bodies.
But the concept of free point and the first principle allow us to set the study of movement, ie mechanics, in a way similar to that with which Euclid had set up the study of spatial properties of bodies: points, lines, plane and solid figures, for Euclid, are not objects of experience, but objects of thought, whose mutual relationships are defined by his famous five postulates.
For example, the following propositions which can be deduced from these postulates:
does not say what are points and lines, the definition of which leads to the paradoxes highlighted by Zeno, but rather they specify the relationships that exist between these objects and implicitly assumes what are the properties of the entity that contains them, ie the geometric space.
Similarly, the concept of free point and the first law of motion allow us to establish a theory of movement, especially because they implicitly define the properties of theoretical entities necessary for its complete and unique description: space, time, reference systems.
The principle of inertia implicitly postulates the properties of space: it is absolute, homogeneous and isotropic.
In fact, to say that a free point, assuming it exists, if it is at rest remains at rest, is the same as to say that, regardless of where it is located (homogeneity), a free body at rest has not a preferred direction to go (isotropy), so it can only remain at rest.
For the Aristotelian philosophers contemporary of Galileo, a free body, wherever he was, should have started to move quickly to reach its "natural place" (unless it was not already in that special point).
Furthermore, the principle of inertia says that, whether a point is stationary, whether it moves in uniform motion, it maintains its state of motion, ie there is no substantial difference between these two situations, so the uniform motion is indistinguishable from rest.
To ensure that a body is at rest, we should make sure that it does not change its position with respect to another body that is certainly at rest.
For the Aristotelian philosophers the question presented no problems. For them, a body at rest surely existed: it was precisely the center of the Universe, ie the center of the Earth. But since Copernicus dethroned the Earth from its privileged role of motionless body at the center of the universe, it was not replaced by anything.
In short, it is impossible to check the status of absolute stillness of a point and then of a frame of reference anchored to it; therefore it is also impossible to determine the absolute motion of a point. The most we can say is that a point P is at rest with respect to a reference system O. The same point P, if described with respect to another reference system O', moving with respect to the first, will appear in motion.
For example, trees and houses are still relative to Earth, but when viewed from a moving train,
they are moving with a velocity opposite to that of the train relative to the Earth.
Moreover, in train stations often happens that if we look out the windows of our train, we do not understand
whether our train is moving (relative to Earth) or the train next to ours.
This confusion, which may seem a deception of the senses, is inevitable and essential in the Newtonian theory.
We can understand that is our reference frame that is accelerating, only if we see, on us or on nearby objects, forces not attributable to traction or pressure by other bodies, which, for example, make us difficult to stand up or make the bags fall down.
If we do not observe forces of this kind (called "fictitious"), the reference frame is said to be inertial.
Forces of this kind are observed only when a reference frame accelerates or decelerates with respect to an inertial reference frame.
When our train (assumed with good shock absorbers) moves with constant velocity relative to Earth, if we keep the windows closed and look only at what happens inside our compartment, we have no sure sign of the movement of the train over the Earth: we can walk, pour a glass of water or throw objects exactly as if we were still relative to Earth.
So the first law of motion implicitly states the existence (at least theoretical) of inertial systems and the theoretical inconsistency of the concept of absolute motion.
Essentially it establishes the principle known as the
Galilean principle of relativity:
If a reference system O' moves with constant velocity with respect to another inertial frame O,
O' is also an inertial system and there is no way of knowing, with internal observations to O',
if this system is at rest or in motion with respect to O.

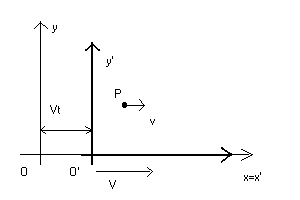
To formalize the considerations in the previous paragraph, let us consider an inertial reference frame with origin O and a frame reference with origin O', which moves with respect to O with a constant velocity V, parallel to the x-axis of the system O.
If, for simplicity, we assume that, at time t0=0, O' coincides with O, then, after a time t, O' will be at a distance X = Vt from O.
Then, at time t, if a point P has abscissa x with respect to O, it has abscissa x'=x-X with respect to O', ie x'= x-Vt.
The other coordinates y and z of P relative to O remain unchanged in the system change, so y'=y and z'=z.
But we must note that in the physics of Galileo and Newton, as in the naive intuition, is taken for granted another thing that will prove controversial: the time runs in the same way in both systems, ie, if in the system O the time elapsed is t, then the time elapsed in the system O' is the same: t'=t.
So, in the foundations of Newtonian mechanics this assumption is also implicit:
the time is the same for all observers; it does not depend on the reference system.
if two events are simultaneous for one observer, they are simultaneous for any other observer.
Summarizing, Newtonian mechanics is implicitly based on the following assumptions:
Given two inertial reference frames O and O', with O' moving with positive velocity V parallel to the x axis of the system O, the space-time coordinates of a point P, from O to O' change in the following way:
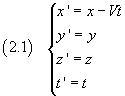
The equations (2.1) are known as the Galilean transformations.
If the point P isn't still with respect to O, but moves with constant velocity v parallel to its x-axis, the velocity v' of the same point with respect to O' is
![]()
The equation (2.2) expresses the principle of addition of velocities, and it is quite easy to be inferred from the Galilean transformations:
![]()
Of course we can also say
![]()
For example, if O' is a train that is moving relative to Earth with a velocity V=30 m/s and P is a passenger on the train that moves with velocity v'=2 m/s relative to the floor of the train, then the velocity v of the passenger relative to Earth is 32 m/s.
If a point P uniformly accelerates and passes from the speed v'1 at the time t'1 to the speed v'2 at the time t'2, its acceleration a' is
![]()
That is, in two inertial reference systems the accelerations are equal.
For the second law of motion, the accelerations are due to forces directly proportional to them. The coefficient of proportionality is the inertial mass of the point.
If, in addition to the three principles of Newton, we assume the principle of conservation of mass, that is that the mass is a constant property of a point, independent of the reference system, from the equality of the accelerations and from the constancy of the mass, we infer, in the inertial reference systems, the equality of the forces.
As long as the physicists limited their studies to the description of the motion of material objects such as planets or molecules or parts of machines such as clocks or engines, Newtonian mechanics in its explicit and implicit presuppositions worked rather brilliantly, corroborating the principles on which it was based, up to make them common sense, obvious, indisputable.
The first doubts began to arise in the nineteenth century when physicists began to deepen the study of the properties of light. These doubts became disruptive with the development of the study of electricity and the formulation, due to Maxwell, of the fundamental equations of electrodynamics.
Limiting the discussion to optics, the most problematic issue was the evaluation of the speed of light.
Galileo, in opposition to the Aristotelians, but also with Cassini and Descartes, who had the opposite opinion, argued that light propagates in space with finite speed and had endeavored to experimentally prove this statement. He could not, because the technical means of the time did not allow the precision required for this measure.
After the first inaccurate astronomical measurements made by Roemer, which, however, led to the conclusion that the speed of light is finite, Fizeau and Foucault, in the mid-nineteenth century, found by laboratory methods for the speed of light in vacuum a value much more accurate, close to 300000 km/s, commonly denoted by c.
By analogy with sound waves, many physicists thought that light, being a wave, could exist only as an oscillation of a continuous elastic medium that is still and fills the whole Universe, which they called ether, and that the speed of light c should be interpreted with respect to the ether.
The conjecture of an ether absolutely at rest is immediately at odds with the foundations of mechanics.
But the principles are not inviolable dogmas. Accepting, provisionally, this conjecture, we must conclude that, if the ether exists and is stationary, in inertial systems moving with velocity V, parallel and equally oriented with the direction of propagation of a light beam, for the Galilean relativity (eq. 2.2), this beam should have velocity c'=c-V.
The problem was carefully studied with increasingly sophisticated instrumentation mainly by the American physicists A. A. Michelson and E. W. Morley, who intended to highlight the existence of the ether.
The negative results of their measurements led A. Einstein's not only to definitely deny the existence of the ether, but also to refine the Galilean principle of relativity, stating that the speed of light in vacuum is the same in all inertial reference frames, ie that the speed of light does not compose with any other velocity. In fact, if in our reference system we would observe that light has speed c' other than c, we could deduce the absolute motion of our system, in blatant contradiction with the Principle of Relativity.
Einstein, however, to confirm and refine the Principle of Relativity, had to deny a fundamental implicit assumptions of Newtonian mechanics, ie the absolute nature of time, replacing it with the principle of absoluteness of the speed of light.
The aim of these physicists was to verify that the speed of light c with respect to the ether
combines itself with the speed V of translation of Earth in its annual movement around the Sun.
For this purpose, they used instruments, called interferometers, which could generate the
interference of two
light beams, produced by splitting a single beam with wavelength λ by a half-silvered mirror and which
covered different optical paths.
When the difference between the optical paths is an integer number of λ, the interference is
constructive;
when the difference between the optical paths is an odd number of λ/2, the interference is destructive.
The interferometer, rigidly connected with the Earth, has the same translation and moves to the right with velocity V.
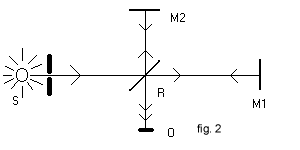
Referring to Figure 2:
If we denote the distance RM1 by d1 and the distance RM2 by d2 and admit the Galilean composition of velocities, we obtain that the beam RM1, when it goes from R to M1, has speed c-V and when it comes back from M1 o R, has speed c+V. The total time t1 it takes to run the the path RM1R is
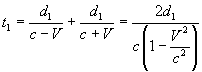
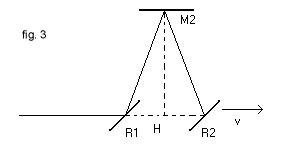
To calculate duration t2 of the path RM2R of the other half beam, we must be observe (Fig. 3) that the forward path RM2 and the backward path M2R do not overlap, because the mirror R is moving. The path R1M2 is not perpendicular to V, but is the hypotenuse of a right triangle with catheti M2H and R1H.
From the Pythagoras' theorem
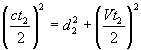
from which
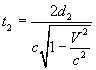
The durations t1 and t2 are different, ie the two beams arrive in O out of phase, producing a sequence of interference fringes.
If the interferometer is rotated by a right angle, in the two expressions of t, d1 and d2 exchange with each other: the phase shift would be different and there would be a different interference pattern.
But this did not happen. Einstein deduced from this that the assumption was wrong, that is the combination of c with V, due to the hypothesis of the existence of ether as an absolute reference system. So he decided to reform the Galilean transformation so that c was constant, regardless of the state of motion of the observer.
The circular functions sinα, cosα and tanα, where α is a real number, are characterized by the following fundamental identities:
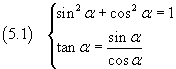
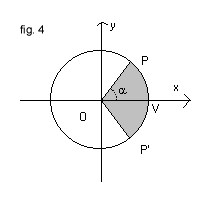
The first of these identities can be deduced by observing (Fig. 4) that in a Cartesian reference frame with origin O, for every counterclockwise angle α, with vertex O and first side ovelapping the x-axis, there is a point P(x,y) of the trigonometric circumference x2+y2=1, and then the coordinates x and y of P are parametric functions of α. Then, we can let
![]()
and substitute these expressions of x and y to the variables in the equation of the circumference.
It should be noted that the parameter α, as well as the amplitude of the angle POV, can be geometrically interpreted as the area of the circular sector POP' where P' is the symmetrical point of P with respect to the axis of abscissas.
A rotation of the reference frame around its origin is a transformation in which each circumference with center at the origin corresponds to itself.
The equations of a rotation of angle α are
![]()
In fact, if we raise to the square both sides of the equations (5.3) and we add the obtained equations, we get x' 2+y' 2=x2+y2
In a similar way let us consider, in the Cartesian plane, the rectangular hyperbola with equation x2-y2=1 (fig. 5).
This hyperbola is formed by two branches that are symmetric with respect to the ordinate axis. Let V be the point in which the right branch intersects the x-axis.
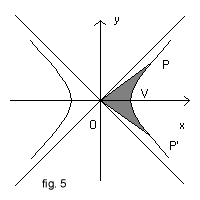
Let P(x,y) be a point of the right branch of the hyperbola and P' its symmetrical with respect to the x-axis and let us consider the figure bounded by the segments OP and OP' and by the arc of hyperbola PVP' (with a dark background in fig. 5).
If we consider positive the area α of this figure when P is in the first quadrant and negative when P is in the fourth quadrant, we can interpret the coordinates x and y of P as parametric functions of α.
The function that gives the abscissa is called hyperbolic cosine (cosh) and the one that gives the ordinate is called hyperbolic sine (sinh).
![]()
If we substitute these expressions of the coordinates to the variables in the equation of the hyperbola and call hyperbolic tangent (tanh) the ratio between hyperbolic sine and cosine, we obtain the fundamental identities for the hyperbolic functions:
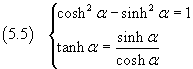
Many other identities could be deduced from these fundamental identities, in a similar way to that followed for the circular functions.
Here, it will suffice to obtain the equalities expressing hyperbolic sine and cosine as functions of the hyperbolic tangent.
For the hyperbolic sine
![]()
and, since the hyperbolic cosine is always positive ≥ 1, then always positive
![]()
In an analogous way, for the hyperbolic cosine
![]()
![]()
A "hyperbolic rotation" is a transformation that transforms a rectangular hyperbola into itself and then it does not affect the expression x2-y2.
The equations of a "hyperbolic rotation" with parameter α are:
![]()
as we can see by squaring both members of the two equations and by subtracting from each other the obtained equations.
As we saw at the end of Section 4, we have to find transformations analogous to those of Galileo, but for which we obtain that the speed of light is independent of the speed of the observer.
For this purpose, let us consider two reference frames with origins O and O' and overlapping x-axes. The origin O' is moving rightward with speed parallel to the x-axes and magnitude V and at the instant when their origins overlap, both of their clocks t e t' give the time 0.
These assumptions must be considered valid in all the following considerations.
At the instant when the origins overlap, a light source, located in the common origin, emits a flash that propagates as a spherical wave with speed c in both reference frames.
In the reference frame O, the position of O' after a time t is Vt, the radius of the spherical wave front is r=ct, the equation of the spherical surface of the front is x2+y2+z2=(ct)2 and the points of this surface on the x-axis are given by the equation x2=(ct)2, ie
![]()
In a Cartesian reference system with orthogonal axes (ct) and x, this equation is represented by a 'rectangular hyperbola' degenerated into a pair of symmetrical straight lines passing through the origin O.
Similarly, in the frame O', the points of the wavefront on the x'-axis are given by the equation
![]()
The transformations we are looking for, must be such that, in the transition from the frame O to the frame O', the expression (ct)2-x2 remains unchanged.
As we saw in section 5, the transformation that leaves unchanged the difference between the squares of the coordinates is the hyperbolic rotation (5.8). In this case, in the equations (5.8), x must be replaced by (ct) and y must be replaced by x: we get
![]()
In the frame O, at time t, the point O' has abscissa Vt; in the frame O' the point O', by definition, has always abscissa 0, then, at time t', O' has abscissa 0.
So, if we consider the point O' and replace its corresponding space-time coordinates in the second of equations (6.3), we obtain
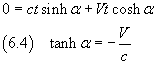
Using this expression of the hyperbolic tangent in the identities (5.6) and (5.7), we have
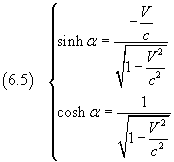
Applying these expressions of the hyperbolic cosine and sine in the equations (6.3), we finally get
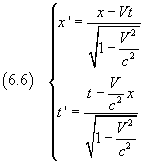
The equations (6.6) express the transformations of the coordinate x and of the time t going from the frame O to the frame O'.
In the situation examined, the y and z coordinates remain unchanged.
These transformations are known as Lorentz equations and must replace those of Galileo (2.1), if we want that the principle of relativity also applies to optics and electromagnetism.
Usually the ratio between V and c is denoted by β:
![]()
In the movements usually studied in classical mechanics, V is many orders of magnitude less than c and thus the ratio β and, a fortiori, its square, are experimentally indistinguishable from 0. In the classical applications the equation (6.6) practically coincide with the equation(2.1).
It is also convenient to introduce the symbol γ, known as Lorentz factor
![]()
so, the four Lorentz equations can be written more succinctly as follows
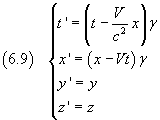
Velocity Addition.
From the Lorentz transformations we can deduce the relation between the speeds which must replace the equation (2.2).
If in the frame reference O a point P has constant rightward velocity with magnitude v, then in the reference frame O', P has velocity v'
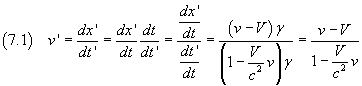
The equation (7.1) is the relativistic law of addition of velocities, which had already been found experimentally by Fizeau.
If, in the equation (7.1), we replace the v on the RHS with c, we obtain c also on the LHS, in accordance with the principle that the speed of light is the same in all inertial reference systems.
c is an asymptote for the relative velocity V
Since any point, moving with constant velocity V with respect to the reference frame O can be considered as origin of a reference frame O', the condition of reality of the Lorentz factor imposes an important physical result: any physical object must move with speed less than c.
Length contraction.
Another important consequence of the Lorentz transformations is the length contraction: moving objects are shorter than when they are motionless.
The length of an object at rest with respect to the observer is called its proper length.
If, in the reference frame O', a bar parallel to the x'-axis has proper length l', at the same time t' one end of the bar has abscissa x'1 and the other has abscissa x'2, with x'2-x'1=l'.
In the corresponding time t, in a system of reference O with respect to which O' moves with velocity V along its x-axis, the bar has length l = x2-x1.
Since
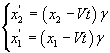
we have
![]()
and then
![]()
that is, the length of the bar in O is shorter than it is in O'.
For example, if with respect to O', which moves with velocity V=0.5c, the length of the bar is l'=10m, in the reference frame O the length of that bar is
![]()
Time dilation.
Similarly, the Lorentz equations imply the phenomenon of time dilation: the duration of a phenomenon, as measured by an observer O' moving with velocity V with respect to an observer O, is greater than the duration of the same phenomenon measured by O.
If, in the frame reference O, the measure of the duration T of the oscillation of a pendulum, suspended at a point with abscissa x=0, begins at time t1= 0 and ends at time t2=T, then in the frame reference O' the same oscillation has duration T' which is obtained from the equations (6.6)
![]()
Since T' is obtained by dividing T by a value less than 1, is T' >T.
For example, if in the reference frame O the pendulum has period T=1s, in the reference frame O', moving with velocity V=0.5c with respect to O, the period of the pendulum is
![]()
We can test this effect experimentally by measuring the lifetime of subatomic particles that are produced in many nuclear reactions.
For example, if an observer O measures the average lifetime of a pion π at rest with respect to himself, he finds a value of 1.77·10-8 s. But if the pion moves relative to the observer O with speed V=0.9c, the measure of its average life is 4.06·10-8 s.
Simultaneity
Another immediate consequence of the Lorentz transformations, quite divergent from common sense, is that, if two events are simultaneous for an observer, they are not for another observer moving with respect to it.
Let us suppose that, with respect to the reference frame O, two events happen at the same time t in two different positions on the x-axis with abscissas x1 and x2.
From the first one of the equations (6.9) we obtain that, with respect to another reference frame O', their times are
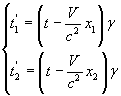
so that
![]()
Their times do not coincide.
Relativistic Doppler effect
See Doppler effect.
The fact that no physical object can move at speed equal or greater than c is not consistent with Newtonian mechanics.
According to Newton, a constant force of magnitude f, acting on a point P with mass m, impresses on it a constant acceleration with magnitude
![]()
and since
![]()
given a constant force, if t→∞, then v→∞, ie, in an appropriate time, P can reach any speed, however high it is.
So we have to change the second law of motion, so as to maintain that, however long a force acts on a particle, the final speed reached by it cannot equal c.
To deduce this result analytically, we ought to state the second law of motion as follows:
a constant force produces a change in momentum that is directly proportional to the force itself and to the duration of its action.
The momentum p of a body with mass m is expressed by the product of mass and velocity: p=mv.
![]()
The change ΔK of the kinetic energy K of a free body is given by the work of the force, ie by the scalar product of force and displacement of the body; since force and displacement are parallel, this scalar product reduces to the product of their magnitudes:
![]()
Based on the results obtained by Planck in his study of the cavity radiation, by Bohr on the atom of hydrogen and by Einstein on the photoelectric effect, we assume that emission and absorption of electromagnetic waves occur with elementary phenomena of transfer of discrete quantities of energy. We call photon each of these amounts of energy, and assume that the energy propagates in the form of photons.
A single photon, from the moment it is generated, moves with constant speed c, so its average speed is c and its energy is
![]()
and its momentum is
![]()
Let us consider the following thought experiment
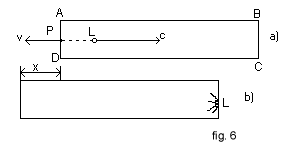
A box, with rectangular section ABCD, is initially at rest with respect to a reference system O, the x-axis of which is parallel to AB. With respect to O, the side AB has proper length l0 and the mass of the box is m0.
At time t=0, a point P, on the face with section AD, emits a photon L rightward (fig. 6).
Exactly as in the case of a gun that fires a bullet, we can apply the principle of conservation of momentum: with respect to O, the box assumes a momentum equal and opposite to that of the photon, and recoils leftward with speed v given by the following identity
![]()
where K is the energy of the photon.
![]()
After his run inside the box, L the photon clashes with the opposite wall, is absorbed and the box stops.
While the box is moving with velocity v, its length l with respect to the reference frame O, from the equation (7.2), is
![]()
Let t be the duration, measured with respect to O, of the flight of the photon.
![]()
At the same time the left face of the box moves leftward, having a displacement x
![]()
Since, while the photon is moving, the box moves to the left, the distance traveled by the photon is lo-x, then
![]()
Equating the expressions (8.6) and (8.8) of t, we obtain
![]()
Substituting into (8.7) the expressions of x, v and t, obtained, respectively, in the equations (8.9), (8.5), (8.6), we get
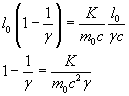
and finally
![]()
The equation (8.10) is the expression of the kinetic energy of a body with rest mass m0, moving at a speed with magnitude v, and should replace the classical
![]()
when the magnitude of the velocity v is an appreciable fraction of c.
If we rewrite the equation (8.10) in the following form
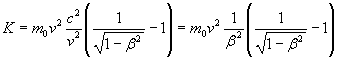
and we calculate the limit of K as β→0, we obtain
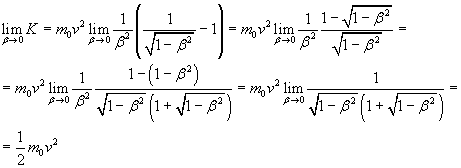
The equation (8.11), ie the classical expression of kinetic energy, is a limiting case of the relativistic expression, valid for velocities v very small with respect to c.
The equation (8.10) can be rewritten also as
![]()
The equation (8.12) shows that the kinetic energy is given by the difference of two terms: the minuend, which will be denoted by E, represents the total energy possessed by the body at the speed v; the subtrahend, which will be denoted by E0, represents the initial energy possessed by the body when it is still.
Unlike theorized by Newtonian mechanics, a free body with mass m0 has, at rest, the energy
![]()
We can easily verify that the total energy
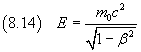
when v=0, coincides with the rest energy.
If in the equation (8.14) we let
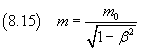
we obtain the expression of the mass m in terms of rest mass mo and speed v.
As we can see, when v increases, also the mass increases, up to approache infinity as v approaches to c.
If we substitute the equation (8.15) in the equation (8.14), we get what surely is the most popular of the relations determined by Einstein, and that may be considered the summary of the theory of special relativity
![]()
Multiplying the expression of the mass (8.15) by v, we obtain the relativistic expression of momentum:
![]()
last revision: 17/11/2015